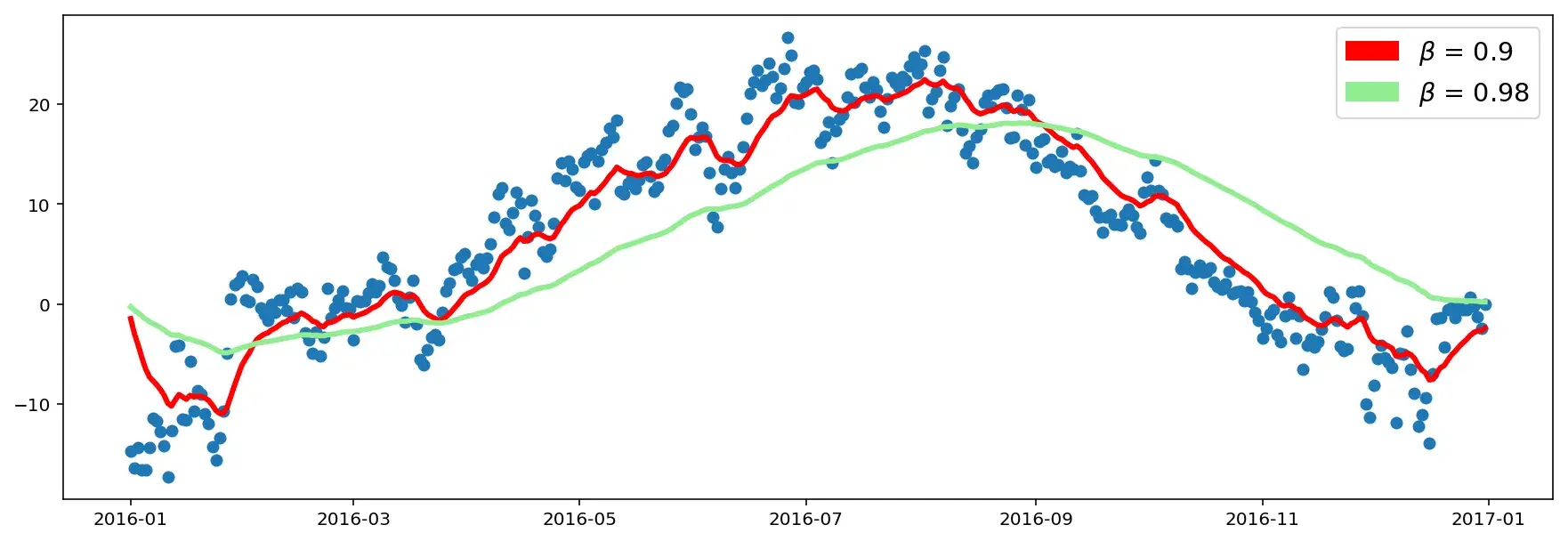
На левой части картинки из предыдущей статьи видно, что в самом начале графика есть весьма очевидная неточность отображения exponentially weighted averages. Слишком сильно отклоняются кривые от скоплений точек.
Когда \(V_0\) инициализируется как \(0\), то \(V_1\) будет вычисляться как:
\[ V_1 = 0.98 V_0+0.02 \Theta_1=0.02 \Theta_1 \]Так как в первый день среднесуточная температура имела значение -14,7°C, значение \(V_1 = 0.02 \cdot (-14.7) = -0.294\). Очевидно, что это довольно неточное усреднение для температуры этого дня.
Для второго дня:
\[ \begin{aligned} V_2 &= 0.98 V_1 + 0.02\Theta_2 = \\ &= 0.98\cdot 0.02\Theta_1 + 0.02\Theta_2 =\\ &=0.196\Theta_1+0.02\Theta_2 \end{aligned} \]Понятно, что это значение также слишком мало.
Для того, чтобы исправить эту неточность, следует воспользоваться формулой:
\[\frac{V_1}{1-\beta^t}\]Поглядим на конкретном примере, какое значение примет знаменатель, в зависимости от дня:
\[t_2: 1-\beta^t=1-(0.98)^2=0.0396\]Тогда значение \(V_2\) будет выглядеть как:
\[\frac{V_2}{0.0396}=\frac{0.0196\Theta_1+0.02\Theta_2}{0.0396}\]То есть можно считать, что bias скорректирован.
Чем больше будет значение \(t\) тем сильнее будет стремиться значение \(\beta_t\) к нулю, тем слабее будет корректировка bias.
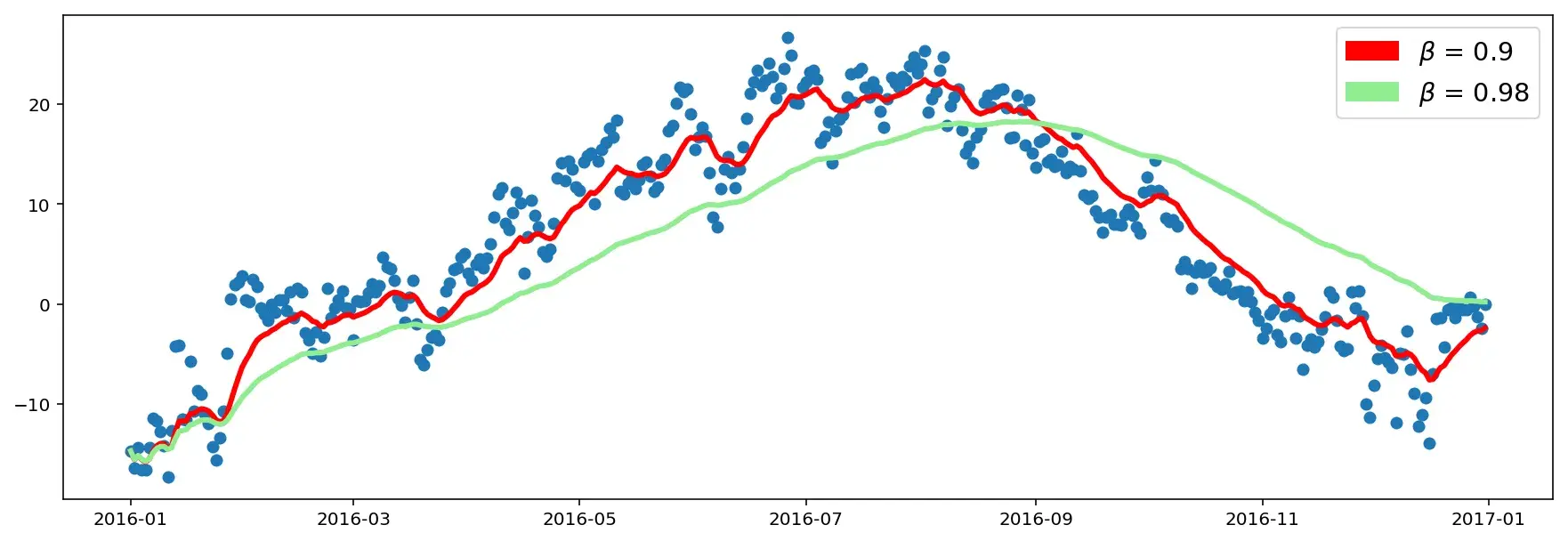
Вот, как будет выглядеть график с корректировкой bias: