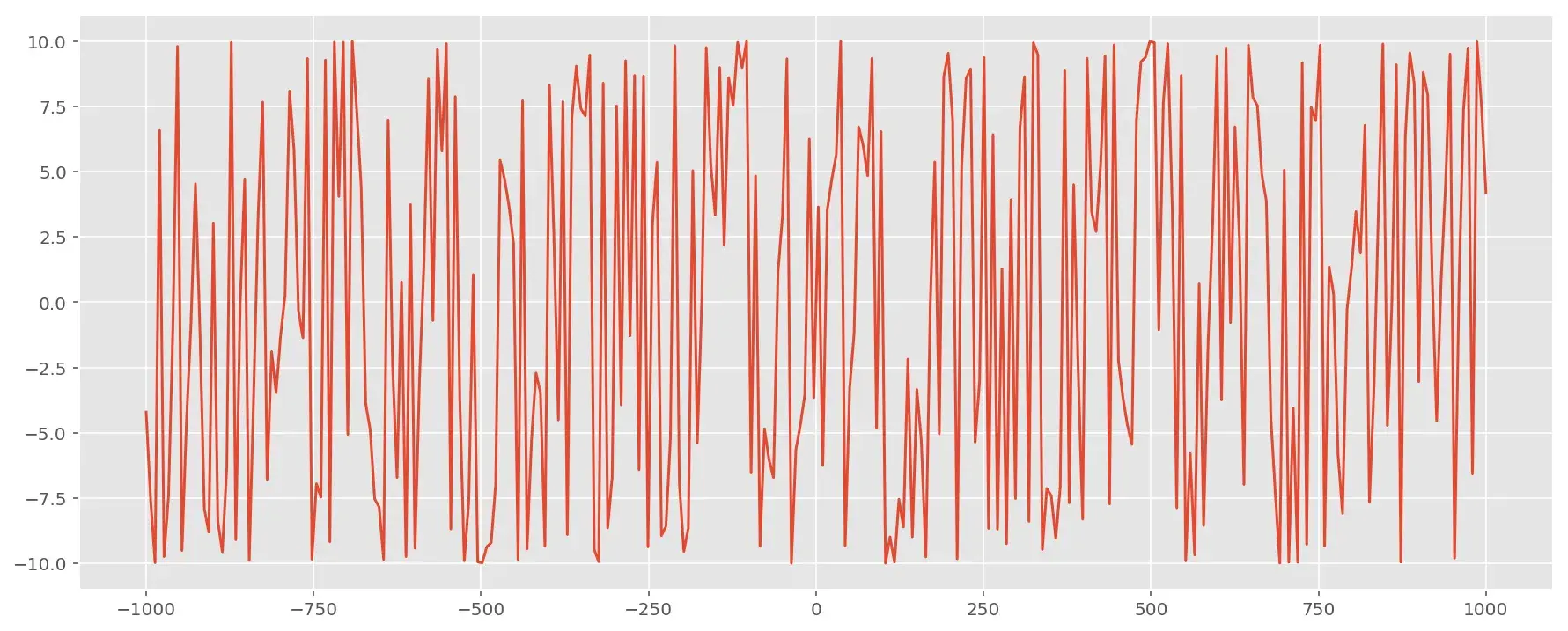
Есть какая-то выборка, распределение которой выглядит, например, как-то так:
Если из этой выборки случайным образом многократно брать подвыборку размера \(n\) и считать ее выборочное среднее:
\[\overline{X}_n=\frac{1}{n}\sum_{i=1}^nX_i\]то окажется, что распределение этих выборочных средних очень близко к нормальному:
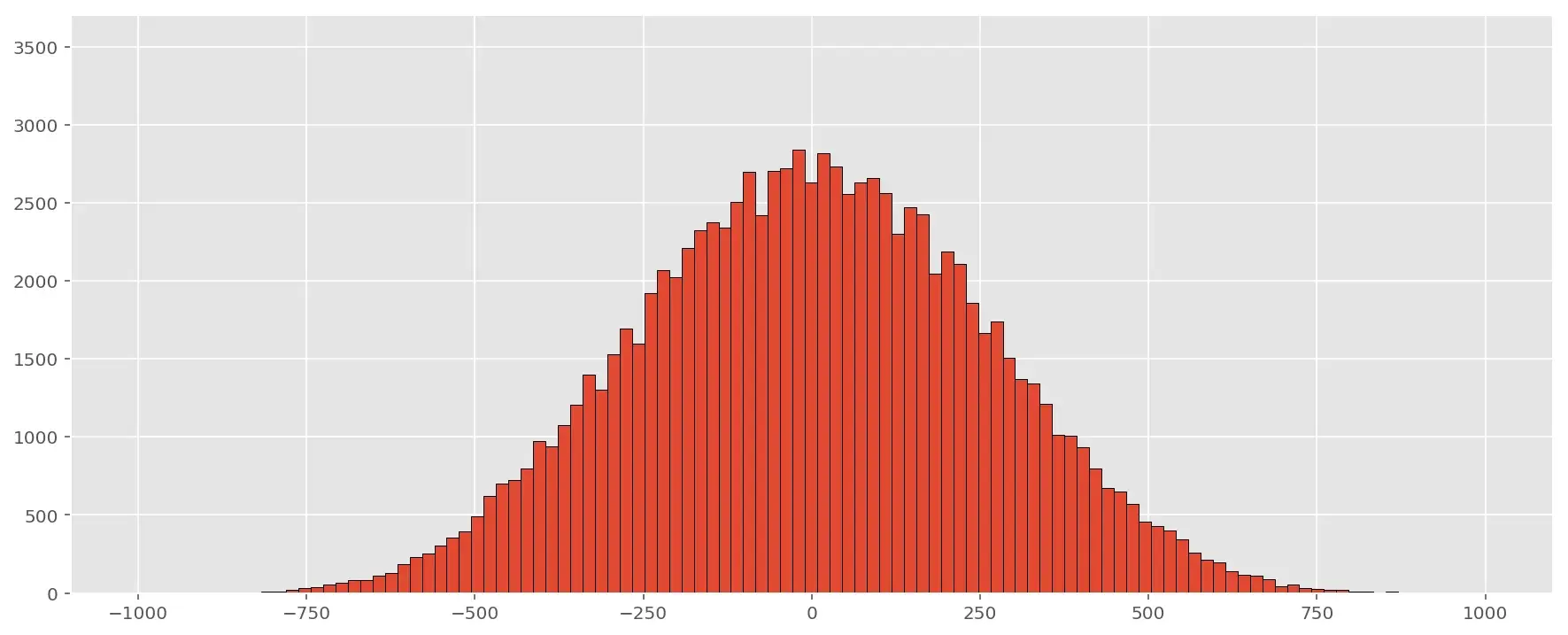
\[\overline{X}_n\approx \sim \mathcal{N}\bigg(\mu,\frac{\sigma^2}{n}\bigg)\]Например, если взять 100000 подвыборок размера \(n=2\), и построить гистограмму распределения средних значений этих подвыборок, она примет вот такой вид:
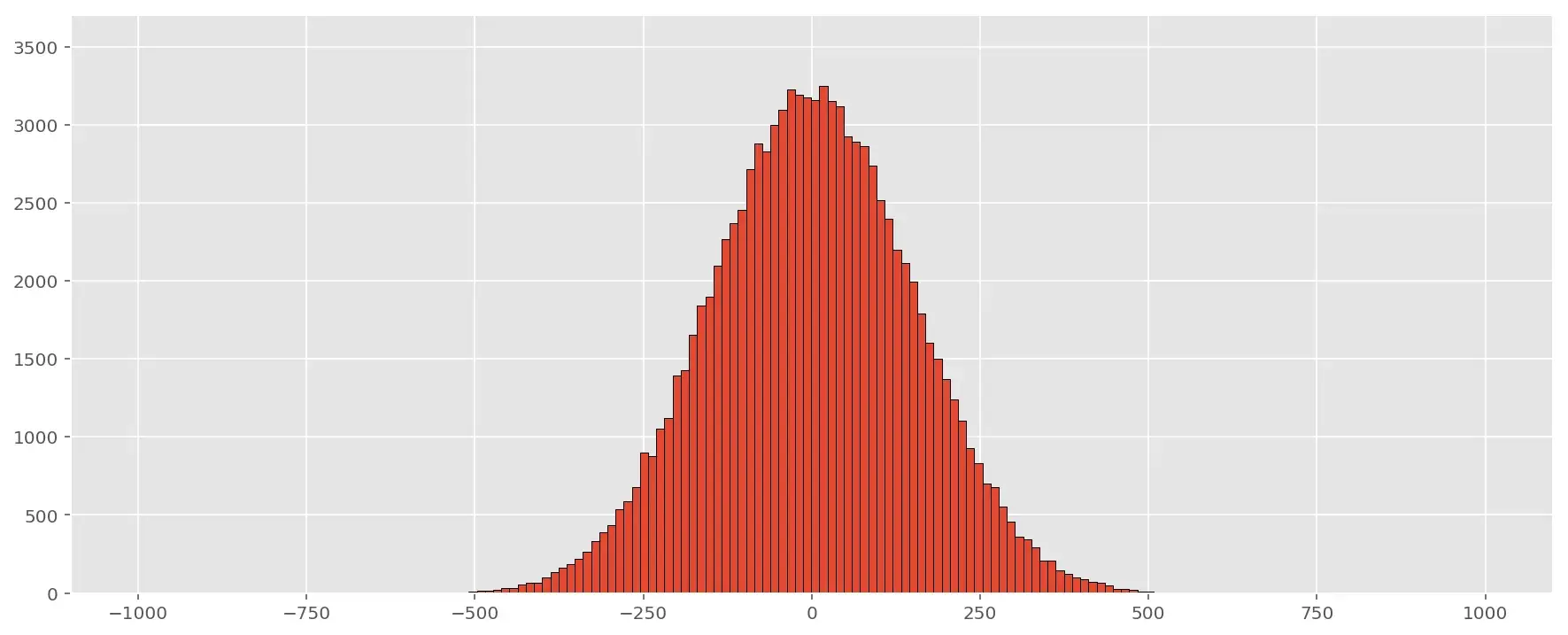
При подвыборках размера \(n=5\):
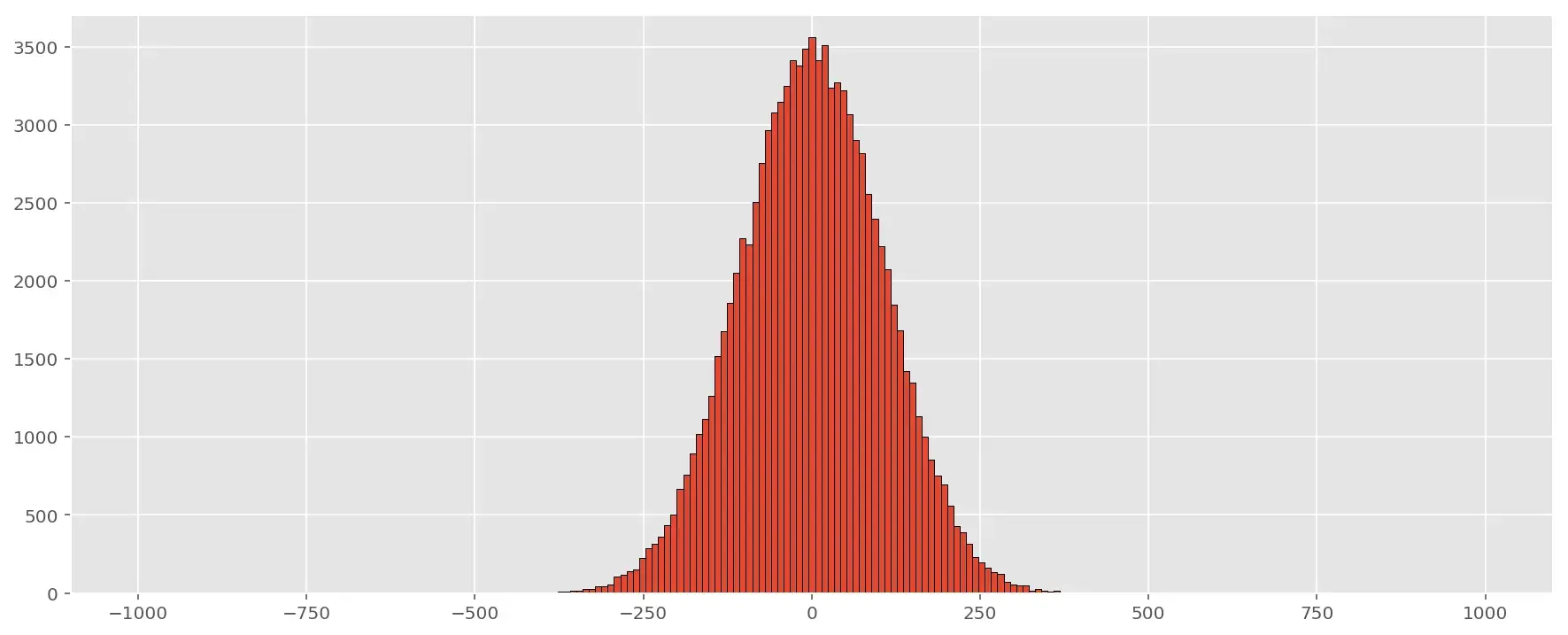
При подвыборках размера \(n=15\):
При подвыборках размера \(n=30\):
На графиках видно, что, при увеличении размера подвыборки, гистограмма все более становится похожа на нормальное распределение и все сильнее прижимается к нулю.