В википедии сказано, что экспоненциальное (или по-другому показательное) распределение — это абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Случайная величина \(X\) имеет экспоненциальное распределение с параметром \(\lambda > 0\), если её плотность имеет вид:
\[f_X(x)= \begin{cases} \lambda e^{-\lambda x}, &x\ge 0 \\ 0, &x<0 \end{cases}\]Параметр \(\lambda\) — это среднее число событий за единицу времени, а среднее значение равно \(\lambda^{-1}\).
Вероятность того, что событие \(T\) наступит раньше какого-то промежутка времени \(t\) считается по формуле:
\[P(T\le t)=1-e^{\lambda t}\]а то, что событие \(T\) случится позже какого-то промежутка времени \(t\):
\[P(T> t)=e^{-\lambda t}\]пример 1
Возьмем такой пример. Есть некий вендор, производящий серверы. Мы посчитали, что в среднем в серверах этого вендора раз в полгода вылетает хотя бы один диск. В этом случае \(0.5\) — это и есть значение параметра \(\lambda\).
Вероятность того, что диск не вылетит дольше какого-то промежутка времени \(t\) можно посчитать как:
\[P(T>t)=e^{-0.5t}\]Например, вероятность того, что в каком-то конкретном сервере не будет сбоя диска в течение года равна:
\[P(T>1)=e^{-0.5\cdot 1}\approx 0.607\]а вероятность, что этот сервер протянет дольше двух лет без единого сбоя диска равна:
\[P(T>2)=e^{-0.5\cdot 2}\approx 0.368\]а вероятность того, что сбоя диска не будет раньше, чем закончится гарантийный срок, который равен трём годам:
\[P(T>3)=e^{-0.5\cdot 3}\approx 0.223\]Вот так будет выглядеть график вероятностей в зависимости от времени:
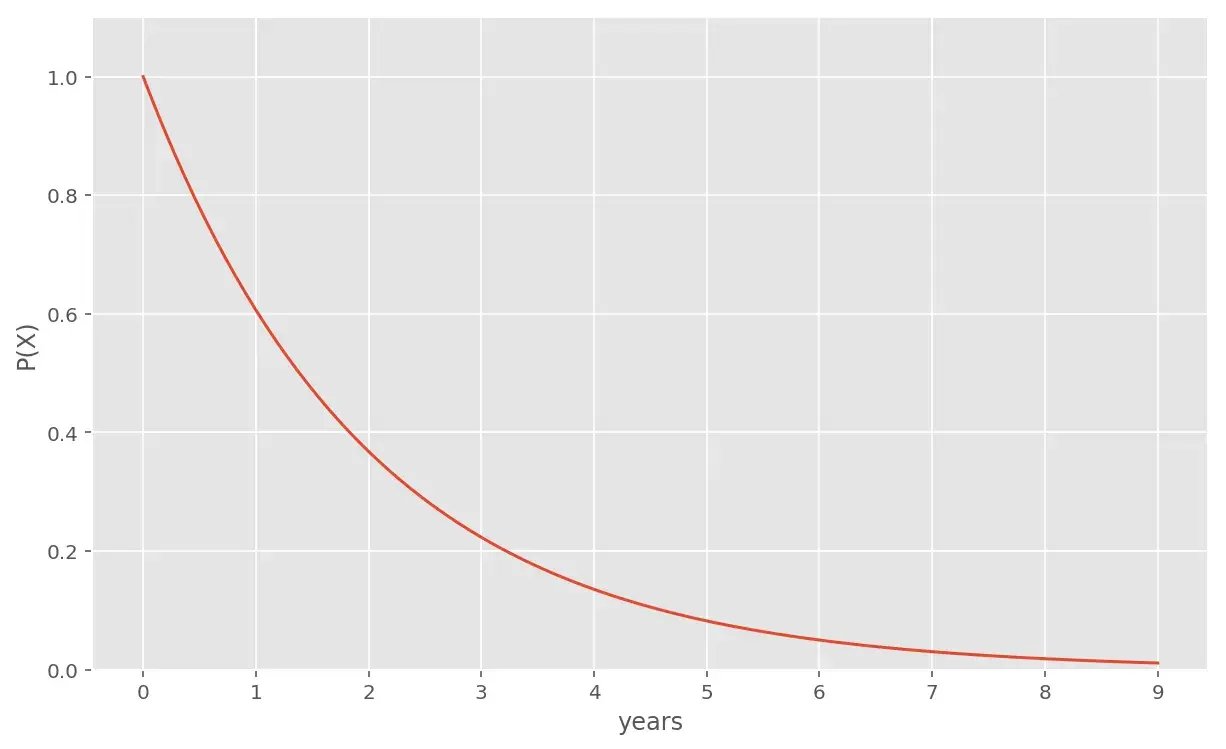
А теперь поглядим на эту проблему с другой стороны: давайте найдем такой промежуток времени \(t\), когда вероятность окажется 5%, то есть \(P(T > k) = 0.05\), или \(P(T \le k) = 0.95\):
\[P(T>k)=e^{-0.5\cdot k}\]если вынести \(k\) за знак равенства:
\[k=\frac{\log(1/0.05)}{0.5}\approx 5.99\]То есть через 6 лет вероятность того, что в сервере вылетит диск, достигнет 95%.
пример 2
В группу технической поддержки в среднем раз в 5 часов приходит инцидент со статусом critical.
вопрос 1
Каково будет значение параметра \(\lambda\) для такой частоты событий?
Так как среднее значение равно \(\lambda^{-1}\), то:
\[\lambda=\frac{1}{5}=0.2\]вопрос 2
Какова вероятность того, что инженер не получит подобный инцидент в течение 6 часов?
\[P(T>6)=e^{-0.2\cdot 6}\approx 0.3\]Вероятность равна 30%.
вопрос 3
Инженер проработал 4 часа и инцидент со статусом critical за это время не пришёл. Какова вероятность, что такого инцидента не будет до конца смены, которая длится 8 часов?
Чтобы ответить на этот вопрос, нужно найти значение условной вероятности \(P(T > 8 | T > 4)\):
\[P(T>8|T>4)=P(T>4)=e^{-0.2\cdot 4}\approx 0.45\]