При решении проблемы k-рукого бандита на каждом временном отрезке \(t\) есть два варианта действий: использование текущего знания о максимальном вознаграждении (exploiting) и исследование (exploring).
Если принять действие на каждом временном отрезке \(t\) за \(A_t\), а соответствующую награду за \(R_t\), то значение ожидаемой награды будет зависеть от выбранного действия \(a\):
\[q_\ast(a) = \mathbb{E}[R_t | A_t = a]\]Если применять жадный (greedy) алгоритм, то каждое действие окажется использованием текущего знания о максимальном вознаграждении. То есть, если у нас есть сведения только об одном вознаграждении на определённом шаге, то нет никаких гарантий, что именно его значение максимально. Так что хорошо бы, хотя бы в некоторых случаях, производить исследование. Для этого введём параметр \(\varepsilon\), который будет отображать вероятность того, что на этом шаге будет произведено исследование. Такой подход называется \(\varepsilon\)-жадным (\(\varepsilon\)-greedy).
Для того, чтобы продемонстрировать преимущество 𝜺-жадного алгоритма перед просто жадным, возьмём десятирукого бандита и инициализируем для него 2000 повторений со случайным ожидаемым вознаграждением, взятым из нормального распределения со средним 0 и стандартным отклонением 1.
q_star = np.random.normal(0, 1, (runs, k))
На каждом шаге требуется принять решение будет ли эксплуатироваться знание или будет проводиться исследование. Для этого генерируется случайное число между нулём и единицей и сравнивается с параметром \(\varepsilon\). Если значение оказывается меньше \(\varepsilon\), то проводится исследование, то есть бандит выбирается из десяти случайным образом. Если значение оказывается больше, то используем жадный алгоритм, выбирая максимально известное значение. Исследование также проводится, если это самый первый шаг.
if Q[problem].sum() == 0 or np.random.random(1) < epsilon:
A_t = np.random.randint(k)
else:
A_t = np.argmax(Q[problem])
Награда на каждом шаге выбирается как случайное значение, полученное из нормального распределения, со средним реальным максимальным значением этого шага и отклонением 1.
R_current = np.random.normal(q_star[problem, A_t], 1)
На каждом шаге оценочное значение вознаграждения считается как усреднённая сумма всех предыдущих вознаграждений:
\[Q_n = \frac{R_1+R_2+\ldots+R_{n-1}}{n-1}\]Это означает, что каждое следующее оценочное значение можно вычислить на основании предыдущего оценочного значения и вознаграждения:
\[ \begin{aligned} Q_{n+1} &= \frac{1}{n}\sum_{i=1}^n R_i =\\ &= \frac{1}{n} \bigg(R_n + \sum_{i=1}^{n-1} R_i\bigg) =\\ &= \frac{1}{n} \bigg(R_n + (n-1)\frac{1}{n-1}\sum_{i=1}^{n-1} R_i\bigg) =\\ &= \frac{1}{n} \big(R_n + (n-1)Q_n\big) =\\ &= \frac{1}{n} \big(R_n + nQ_n - Q_n\big) =\\ &= Q_n + \frac{1}{n} \big(R_n - Q_n\big) \end{aligned} \]То есть, в общем случае, значение обновляется на каждом шаге на разницу между текущей наградой и ожидаемым значением, умноженную на некий коэффициент размера шага. В этом конкретном случае коэффициент динамический и уменьшается с каждым новым шагом.
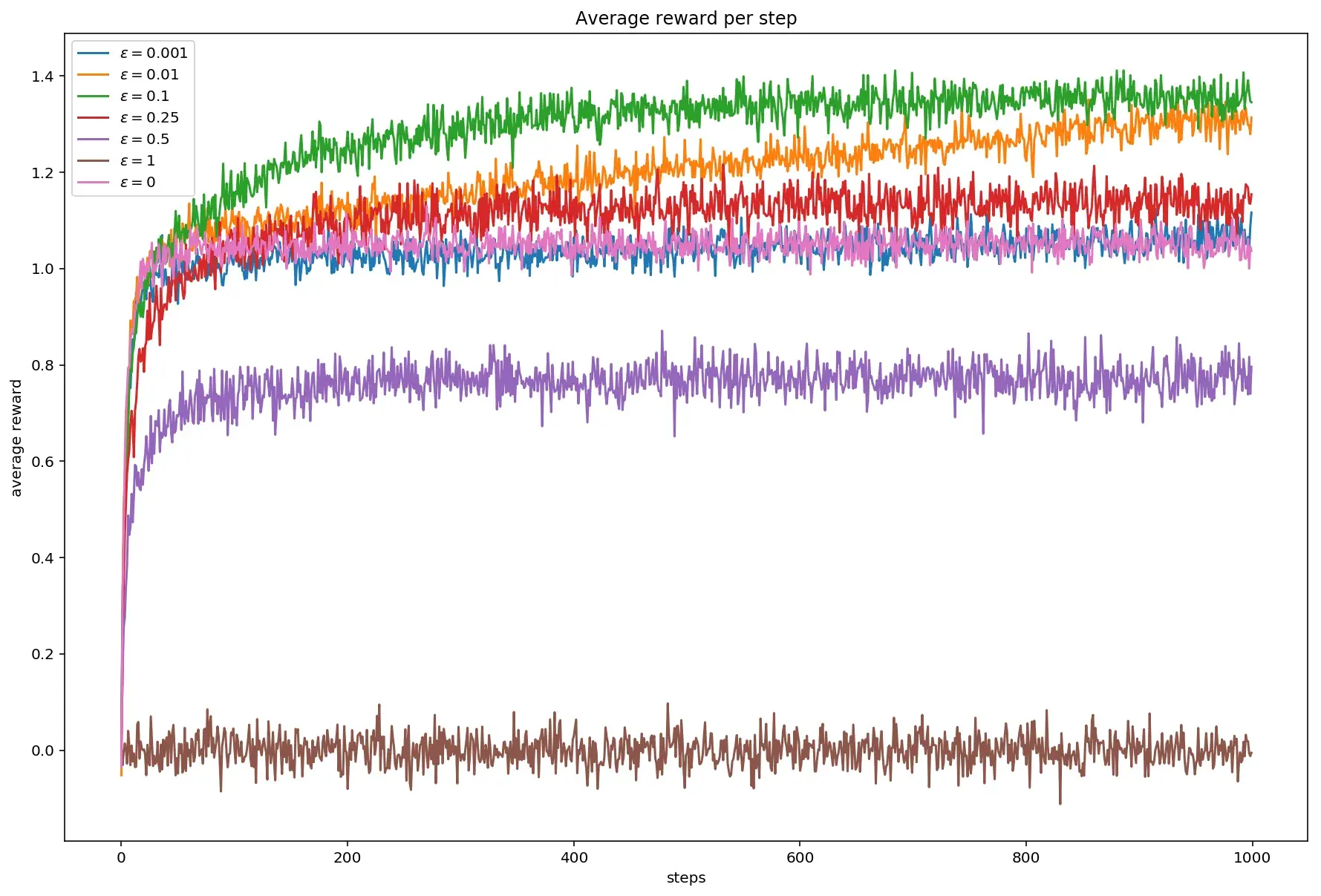
А теперь поглядим на графики. Очень любопытно выглядит средняя награда при разных значениях \(\varepsilon\).
Максимальное значение достигается при \(\varepsilon\) равном 0.1.
При \(\varepsilon\) равном нулю, то есть при включении жадного алгоритма, среднее значение колеблется в районе единицы, впрочем, как и \(\varepsilon\) равном 0.001.
В случае, когда \(\varepsilon\) равен единице, то есть каждый раз действие оказывается исследовательским, среднее значение колеблется в районе нуля.
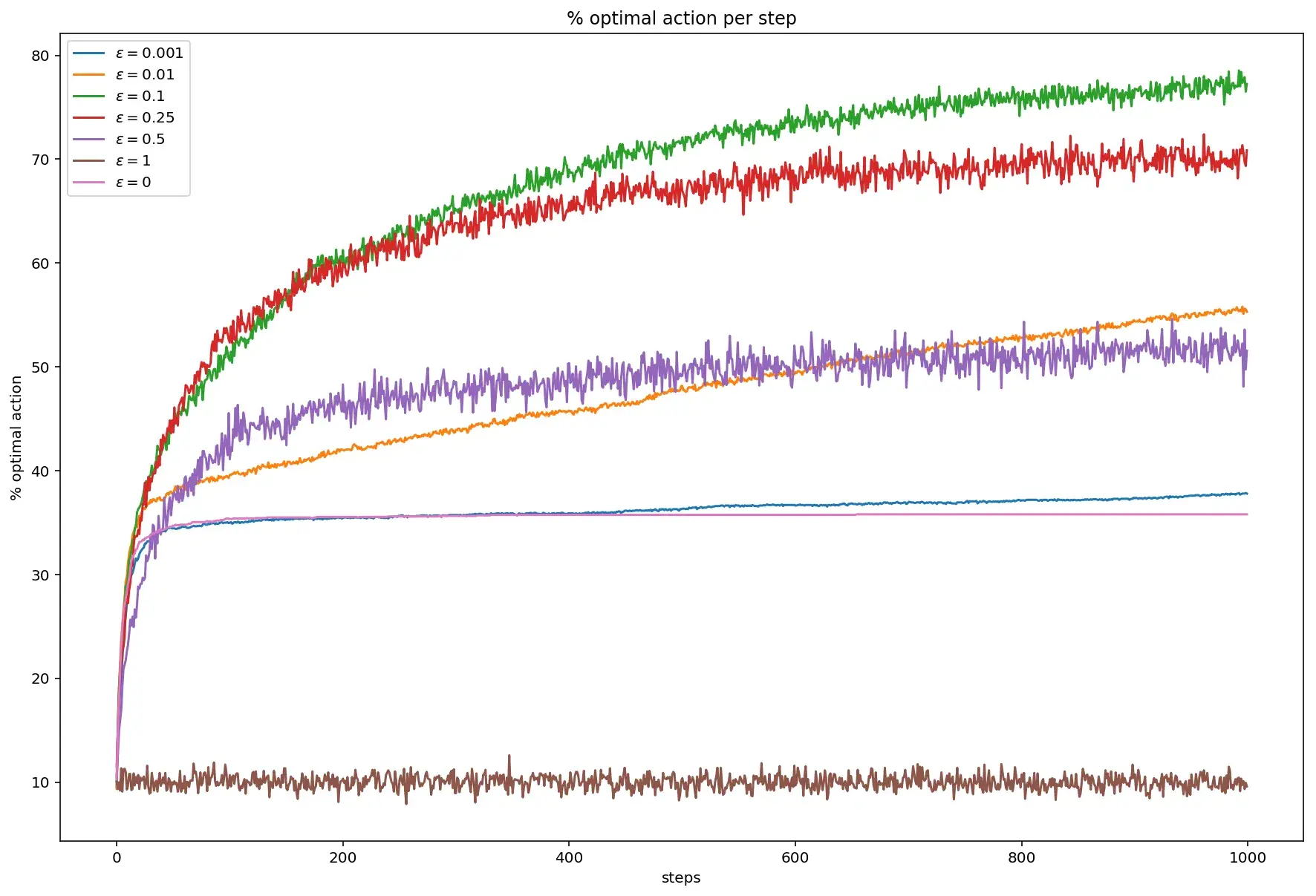
На следующем графике показан процент оптимальных действий, то есть таких действий, в результате которых было выбрано максимально возможное значение для каждого шага.
Опять же, максимальные значения достигаются при \(\varepsilon\) равном 0.1. При жадном действии, значение колеблется в районе 30%, а при \(\varepsilon\) равном единице — в районе 10%.
https://github.com/kukumber/k-armed_epsilon-greedy/blob/master/k-armed_epsilon-greedy.ipynb