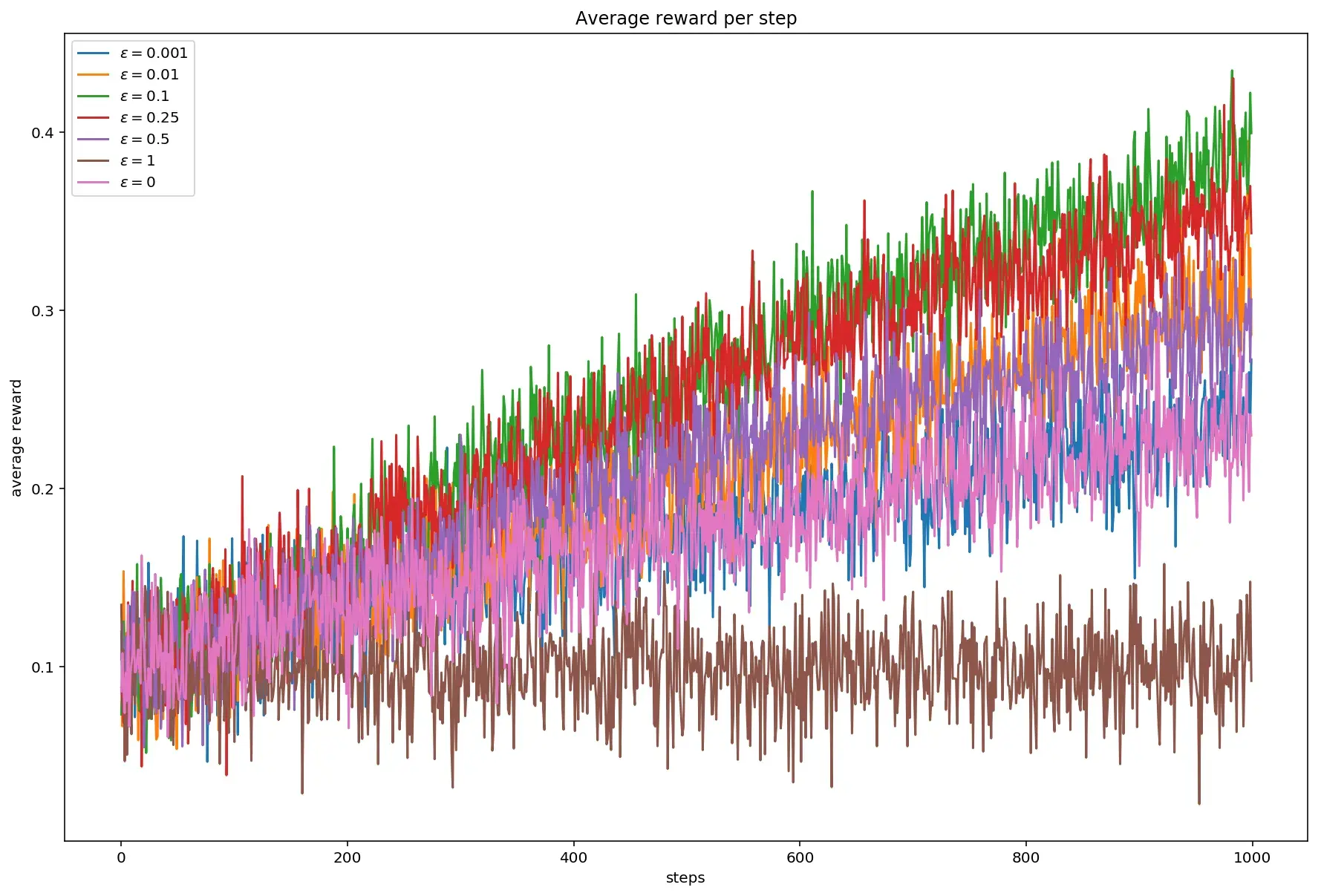
Представим, что ситуация немного поменялась и началась флуктуация реальных ожидаемых наград, то есть они перестали быть стационарными, как в предыдущем случае.
Допустим, исходные значения ожидаемых наград заданы одинаково, например, они равны 0.1, и на каждом шагу к ним начало прибавляться случайное число, взятое из нормального распределения со средним 0 и стандартным отклонением 0.01.
q_star[problem] += np.random.normal(0, 0.01, k)
В этом случае всё становится, мягко говоря, очень печально.
У средней награды пропадает резкий скачок вверх на первом десятке шагов, а сам график становится практически линейным для любого значения \(\varepsilon\) (ср. с графиком в предыдущей статье).
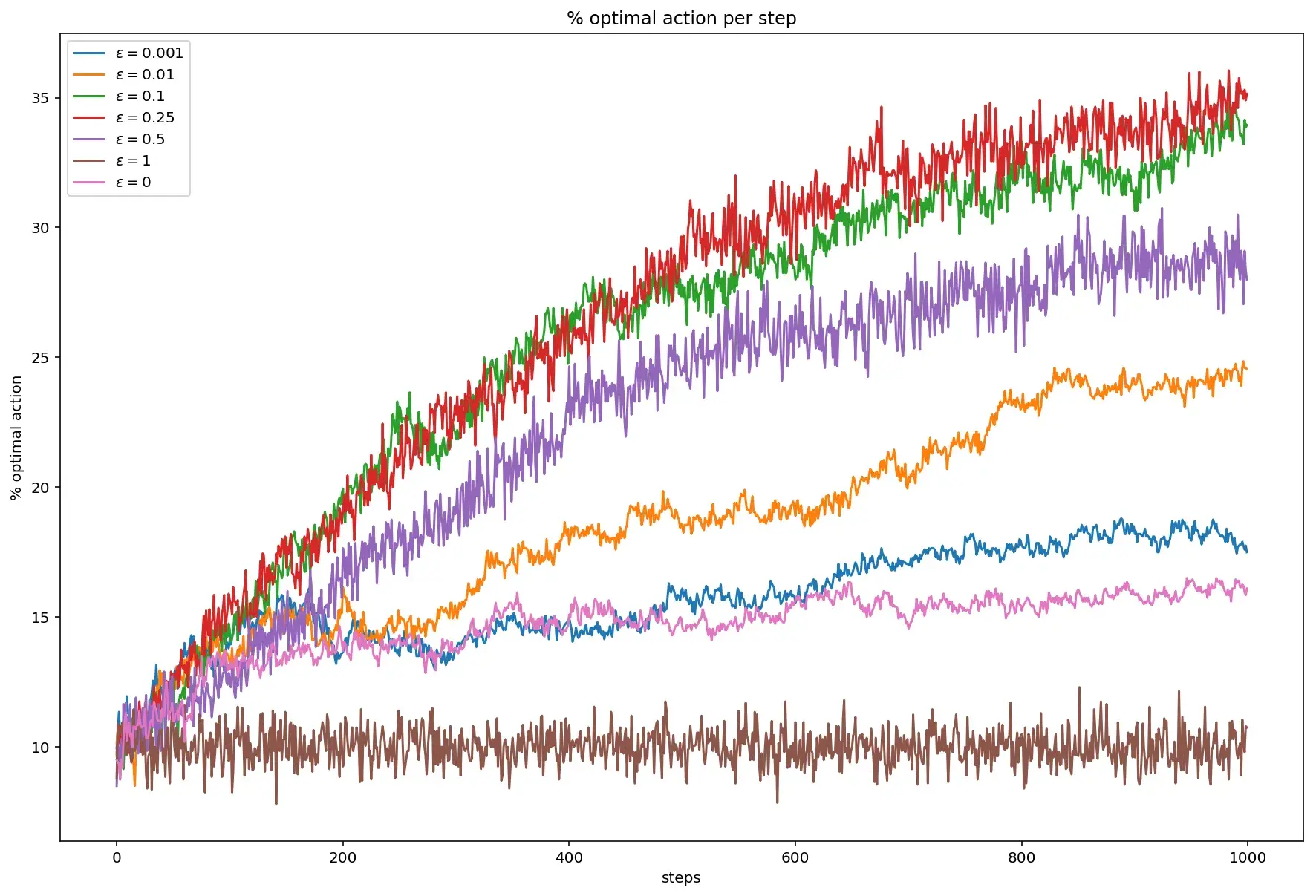
Процент выбора оптимального действия тоже значительно падает:
Если в стационарном случае максимальный процент начинал подбираться к отметке 80%, то здесь, в лучшем случае он добирается до 35%.
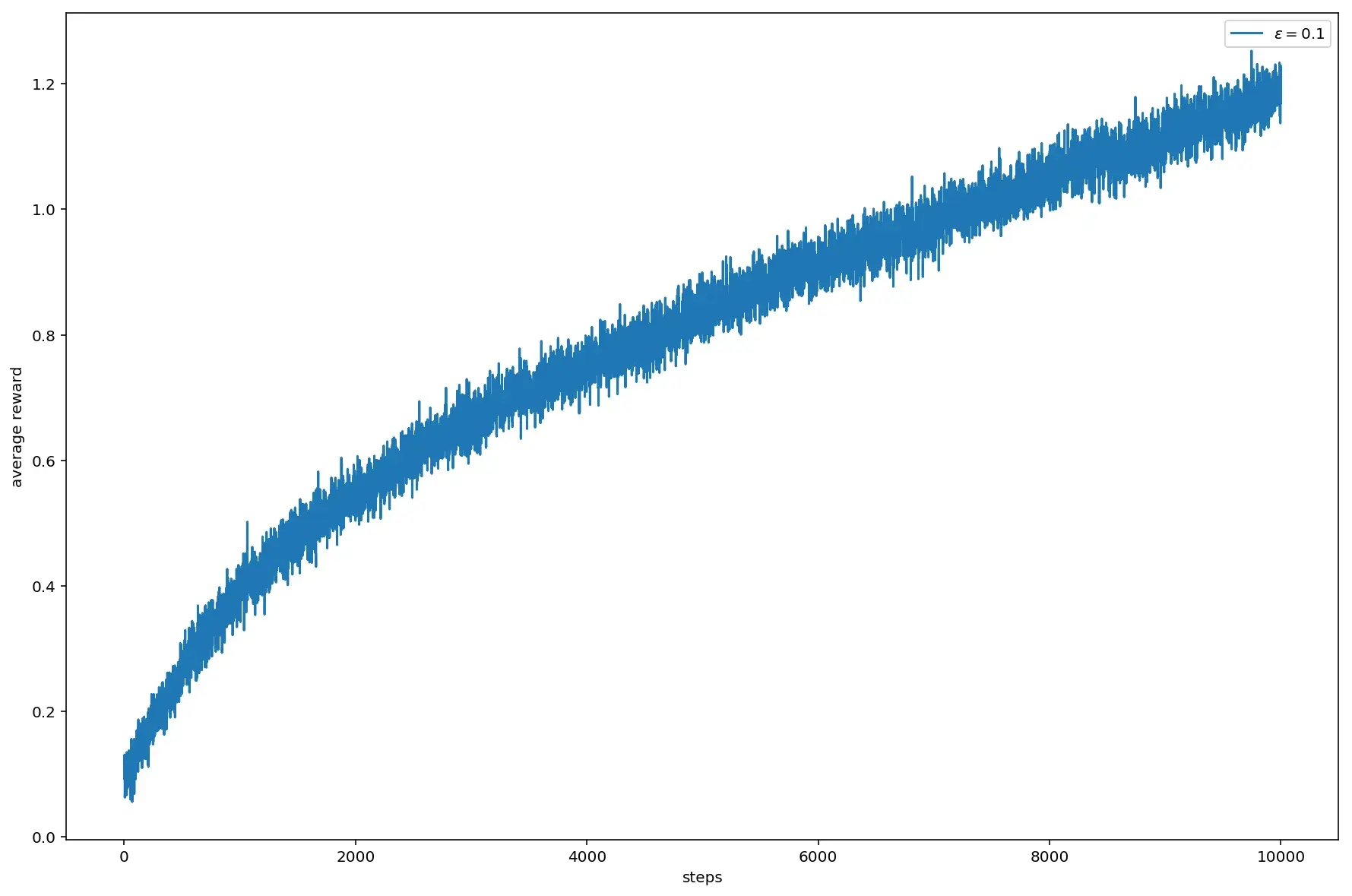
Первое, что следует попробовать — увеличить количество шагов. Так как считается довольно долго, оставим один параметр, показавший наилучшие значения в стационарном случае, то есть \(\varepsilon = 0.1\):
Получается, что для того, чтобы начать приближаться к результатам стационарного случая, при котором максимум близкий к 1.4 достигался за 1000 шагов, количество шагов пришлось увеличить на порядок. При этом максимально среднее качество приблизилось к 1.2.
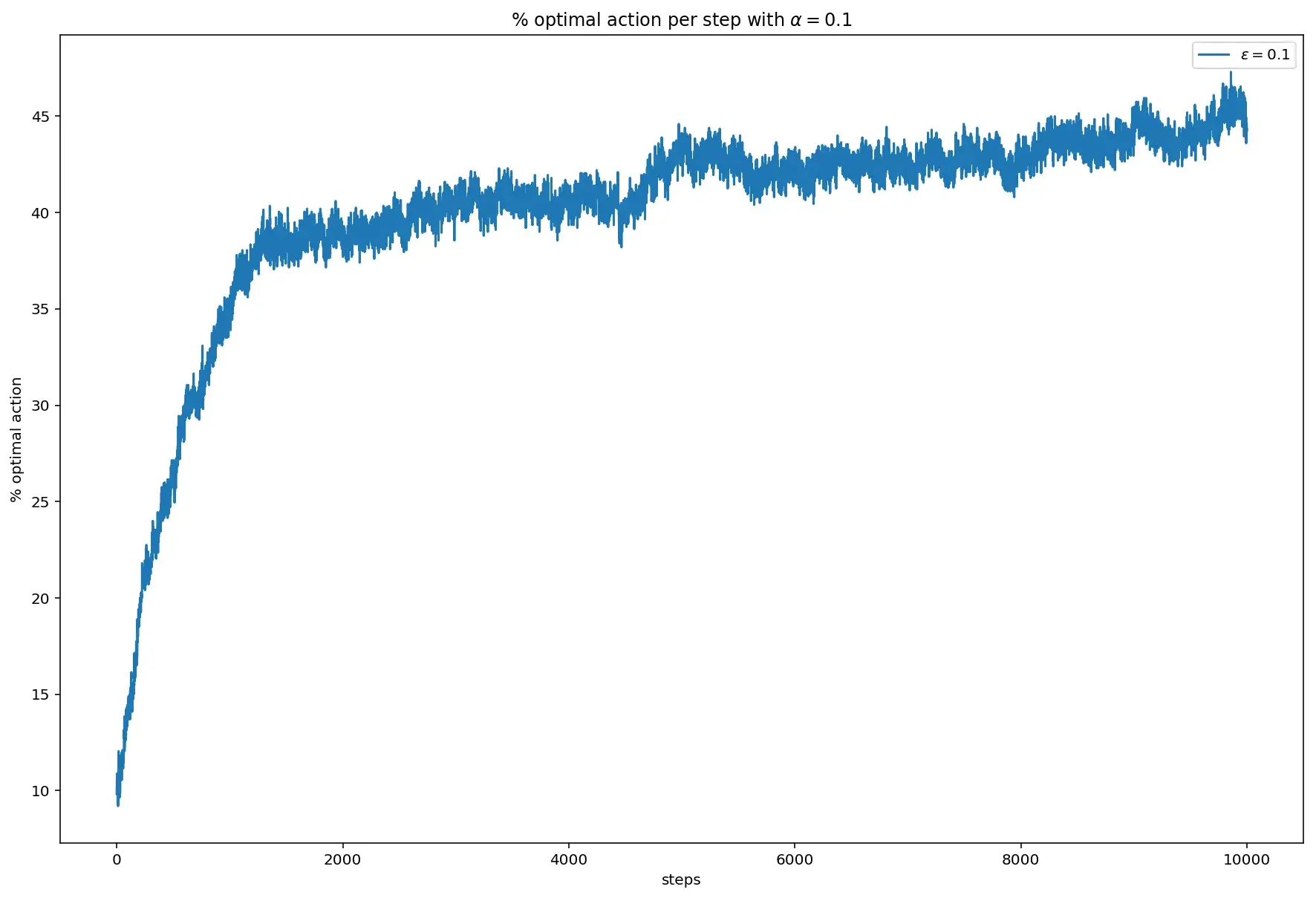
При этом процент оптимального выбора за 10000 шагов едва добрался до 45% (в стационарном случае он был где-то в районе 75%):
Оказывается, эту проблему можно решить при небольшого изменения формулы оценочного вознаграждения, которая выглядит вот так:
\[Q_{n+1} = Q_n + \frac{1}{n}\big[R_n-Q_n\big]\]В этой формуле присутствует, меняющийся на каждом шагу коэффициент \(1/n\). Заменим его на постоянный коэффициент \(\alpha\):
\[Q_{n+1} = Q_n + \alpha[R_n-Q_n]\]и поглядим, как изменится при этом поведение графика функции:
Заменив коэффициент на постоянную и увеличив количество шагов до 10000, удалось добраться до тех значений, которые были получены в стационарном случае.
Процент оптимального выбора при этом значительно повысился:
Значение увеличилось с 45% до 75%.
Можно сделать вывод, что в случае, когда значение ожидаемой награды изменяется на каждом шагу, ситуацию может спасти значительное увеличение количества шагов и замена коэффициента на константу.