Логистическую регрессию можно использовать в тех случаях, когда нужно произвести бинарную классификацию, то есть, алгоритм на выходе должен выдать 1 или 0.
Допустим, есть некий вектор \(x\), который содержит в себе информацию об изображениях. Глядя на эти данные, нужно распознать, например, есть ли на картинке машина или нет. Алгоритм на выходе должен выдать вероятностное предсказание \(\hat{y}\):
\[\hat{y}=P(y=1|x)\]Другими словами, если \(x\) — это картинка, алгоритм должен показать, какова вероятность того, что на этой картинке есть машина.
Вектор \(x\) имеет размерность \(n_x\):
\[x\in\mathbb{R}^{n_x}\]Вектор параметров \(w\) также имеет размерность \(n_x\):
\[w\in\mathbb{R}^{n_x}\]Параметр \(b\) — это вещественное число:
\[b\in \mathbb{R}\]Имея все это добро, можно попытаться сгенерировать \(\hat{y}\) при помощи линейной функции:
\[\hat{y}=w^Tx+b\]Но это точно не заработает, потому что при бинарной классификации нужна вероятность принадлежности к классу, то есть \(0 \le \hat{y} \le 1\), а линейная функция выдает на выходе любые значения: большие, маленькие, положительные, отрицательные.
Для логистической регрессии то, что возвращается линейной функцией, отправляется на вход сигмоиде:
\[\hat{y}=\sigma(w^Tx+b)\]Если линейную функцию для удобства присвоить переменной \(z\):
\[z=w^Tx+b\]То уравнение сигмоиды будет выглядеть вот так:
\[\sigma= \frac{1}{1+e^{-z}}\]А вот как сигмоида выглядит на графике:
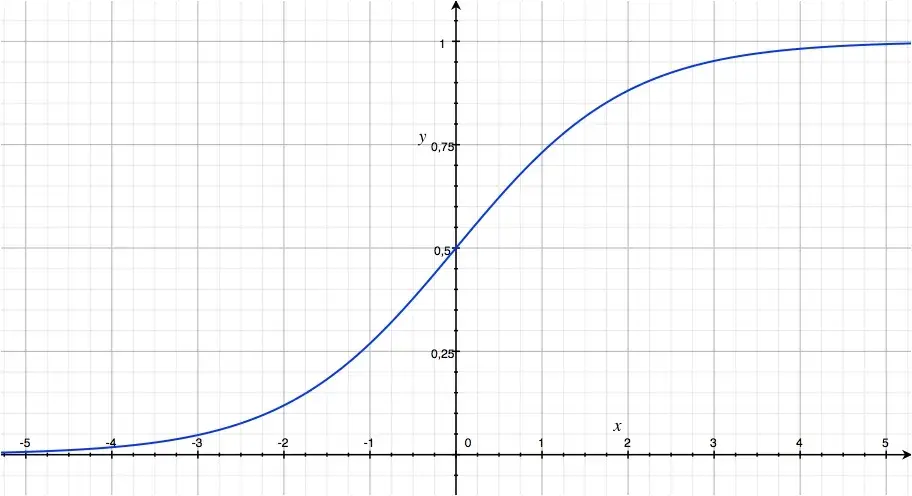
Если значение \(z\) велико, то \(e^{-z}\) будет близко к нулю, а значение \(\sigma(z)\) будет стремиться к единице.
Если значение \(z\) очень маленькое или отрицательно, то \(e^{-z}\) будет иметь большое значение, а \(\sigma(z)\) будет стремиться к нулю.
Строго говоря, сигмоида — это не одна функция, а целый класс функций, которые обладают общими свойствами: гладкостью, монотонностью, непрерывностью и внешним видом, схожим с буквой S. Однако, чаще всего, под термином “сигмоида” подразумевают именно логистическую функцию, формула которой указана выше.