Для того, чтобы натренировать параметры \(w\) и \(b\) для логистической регрессии, нужа cost function.
У нас есть \(m\) примеров:
\[\big\{(x^{(1)},y^{(1)}),\ldots,(x^{(m)},y^{(m)})\big\}\]на которых будет тренироваться функция и нужно, чтобы параметры \(w\) и \(b\) были такими, чтобы предсказание \(\hat{y}^{(i)}\) было максимально близко к правильному ответу \(y^{(i)}\), то есть \(\hat{y}^{(i)}\approx y^{(i)}\).
То есть для каждого тренировочного примера \(i\):
\[\hat{y}^{(i)} =\sigma(w^Tx^{(i)}+b)\]и, соответственно:
\[\sigma(z^{(i)})=\frac{1}{1-e^{-z^{(i)}}}\]где \(z^{(i)}\):
\[z^{(i)}=w^Tx^{(i)}+b\]loss function
Loss function (функция потерь), измеряющая то, насколько хорошо работает алгоритм, может быть представлен, например, среднеквадратичной ошибкой:
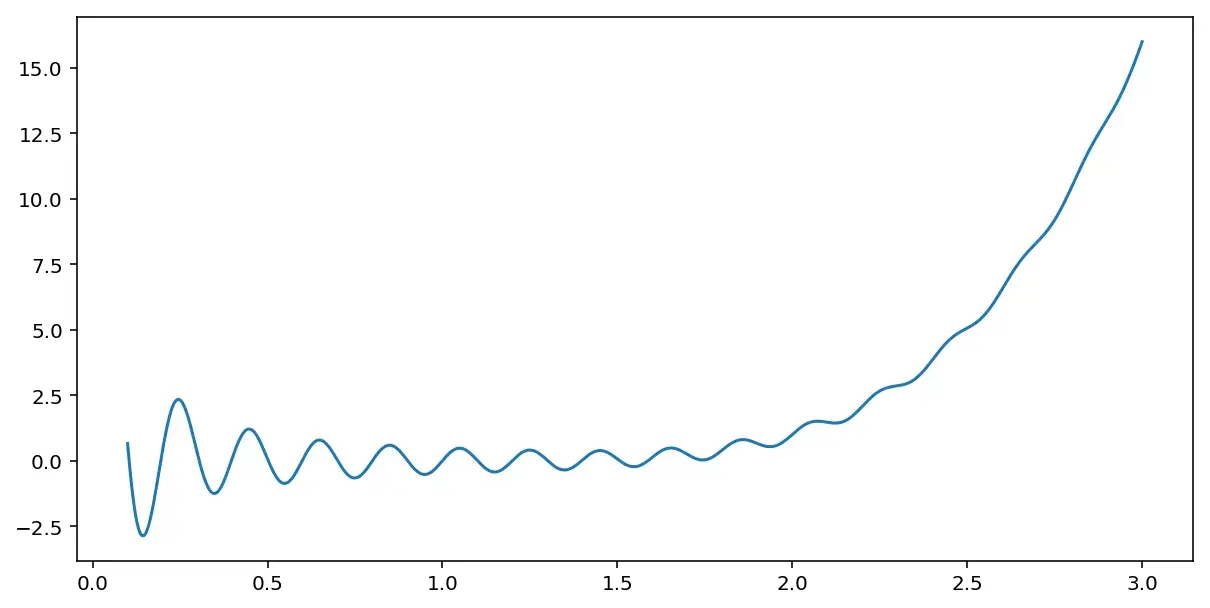
\[\mathcal{L} (\hat{y}, y) = \frac{1}{2}\big(\hat{y}-y\big)^2\]Однако, при таком подходе легко может оказаться, что оптимизационная проблема невыпуклая и у нее множество локальных оптимумов и градиентный спуск не сможет найти глобальный оптимум. Она может выглядеть как-нибудь так:
Главное, что следует понять, что loss function — это способ измерить то, как хорошо функция предсказывает \(\hat{y}\) для каждого конкретного y и необходимо сделать так, чтобы эта функция оказалась минимально возможной.
Для логистической регрессии используется иная loss function, которая делает оптимизационную проблему выпуклой, и на которой градиентный спуск сможет найти глобальный оптимум.
Для логистической loss function обычно используют такую формулу:
\[\mathcal{L} (\hat{y}, y) = -\big(y\log\hat{y}+ (1-y)\log(1-y)\big)\]Если \(y = 1\), то правая часть суммы окажется равной нулю и loss function приобретет вид:
\[\mathcal{L} (\hat{y}, y) = -\log\hat{y}\]В этом случае нужно будет стремиться к тому чтобы переменная \(\hat{y}\) имела максимально возможное значение. Так как \(\hat{y}\) — это сигмоида, а ее значение не может быть больше единицы, то есть нужно, чтобы значение \(\hat{y}\) было как можно ближе к единице.
Если \(y = 0\), то левая часть суммы окажется равной нулю и loss function будет выглядеть так:
\[\mathcal{L} (\hat{y}, y) = -\log(1-\hat{y})\]В этом случае, наоборот нужно стремиться к тому, чтобы значение переменной \(\hat{y}\) было как можно меньше.
cost function
Теперь перейдем к тому, как измерить точность работы алгоритма по всем возможным примерам. Измерять эту точность будет cost function:
\[\mathcal{J}(w,b)=\frac{1}{m}\sum_{i=1}^m\mathcal{L}(\hat{y}^{(i)},y^{(i)})\]То есть cost function — это среднее арифметическое всех значений loss function, которые посчитаны для каждого тренировочного примера.