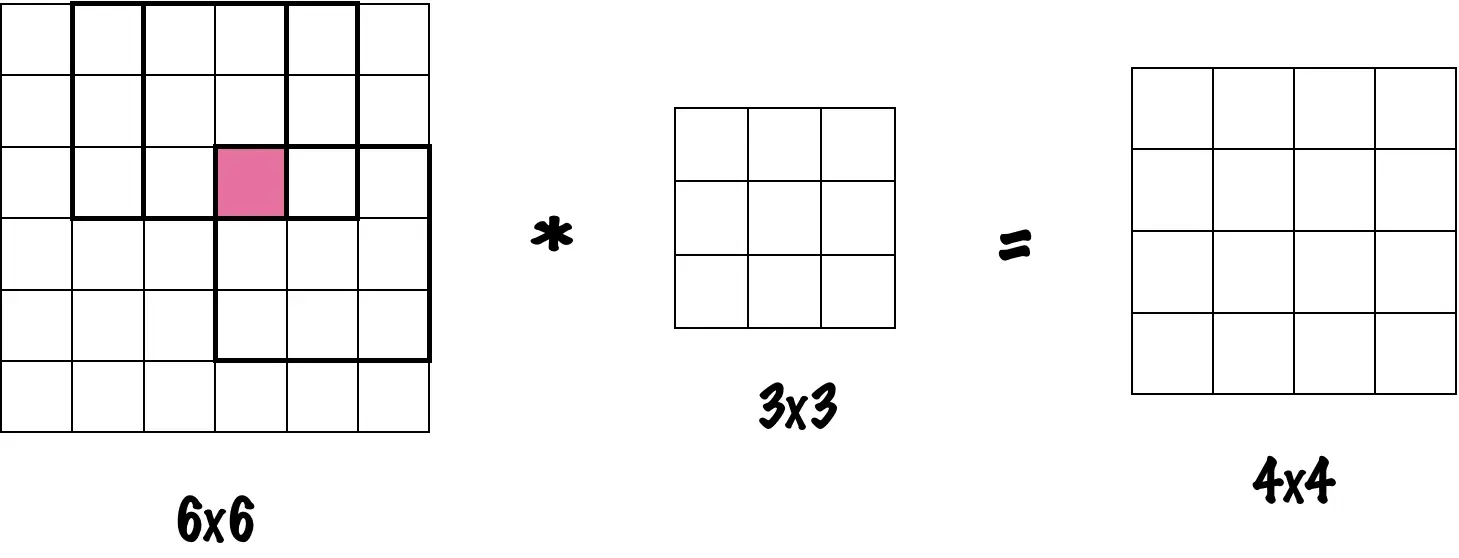
Если взять изображение размера 6 x 6 пикселей и провести над ним операцию свертки при помощи фильтра размера 3 x 3, то на выходе получится уменьшенное изображение размера 4 x 4:
Так произойдет потому, что для фильтра размера 3 х 3 есть всего лишь 4 х 4 возможных положений. В общем случае, если есть картинка размера n x n, к которой применяется фильтр размера f x f, то на выходе получится картинка с разрешением:
\[(n-f+1)\times (n-f+1)\]Основное следствие этого факта — каждое применение свертки уменьшает размер изображения.
Другое следствие — угловые пиксели изображения имеют минимальное влияние на операцию свёртки, потому что они задействуются только единожды, когда фильтр применяется в углу. Пиксели по краю изображения тоже оказывают минимальное информационное влияние на процесс свертки.
Тогда как пиксели в центре попадают под действие фильтра многократно:
Для решения этих двух проблем: проблемы уменьшения исходного изображения и проблемы пикселей в углах и по краям изображения, придумана техника padding — добавление дополнительного пикселя (или нескольких) по краю изображения. То есть, добавив изображению 6 х 6 по краю один пиксель, обычно с нулевым значением, можно добиться того, что после применения фильтра 3 x 3 на выходе получится исходное разрешение 6 х 6:
Для свертки с padding разрешение финального изображения будет считаться по формуле:
\[(n+2p-f+1) \times (n+2p-f+1)\]где \(p\) — это количество добавленных пикселей.
В существующей терминологии свёртка может быть valid или same.
Valid — это свертка без padding, то есть без добавления дополнительных пикселей.
Same — это свертка с таким значение padding, что на выходе получается изображение с разрешением исходного изображения.
Для того, чтобы посчитать, каким должен быть padding для случая same, можно воспользоваться формулой:
\[p = \frac{f-1}{2}\]По причине того, что в знаменателе стоит двойка, фильтр обычно подбирается нечётный. Если фильтр чётный, то нужно идти на дополнительные ухищрения и подбирать ассиметричный padding.