Плотность распределения вероятностей непрерывной случайной величины нужна для того, чтобы показать изменение вероятности на каком-то конкретном элементе множества. Плотность распределения — это производная от функции распределения непрерывной случайной величины:
\[f(x)=F'(x)\]У дискретных (принимающих конечное или счетное число значений) величин плотности нет.
Вероятность того, что непрерывная случайная величина примет значение от \(a\) до \(b\) равна интегралу от \(a\) до \(b\) плотности распределения случайной величины:
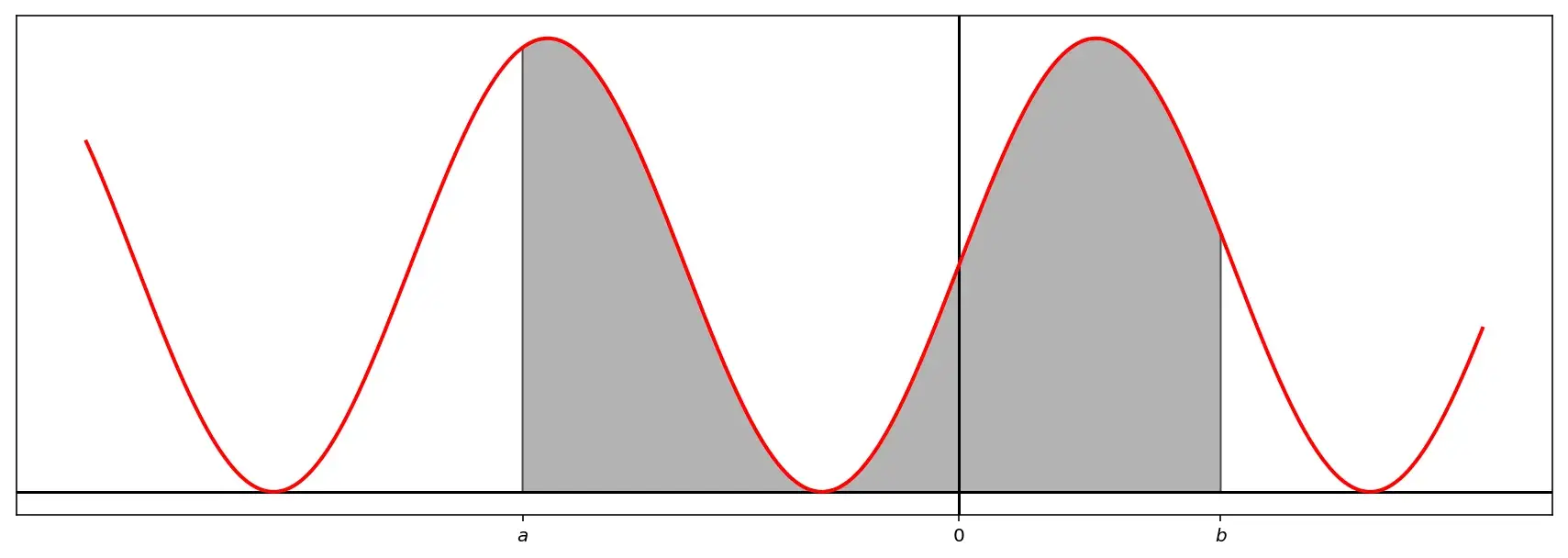
\[P(a\le X \le b)=\int_a^b f(x)dx\]А вот так это можно показать геометрически. Допустим, есть некая плотность распределения случайной величины:
Вероятность того, что \(X\) примет значение от \(a\) до \(b\), равна площади фигуры под кривой в диапазоне как раз от \(a\) до \(b\) (на графике эта площадь показана серым).
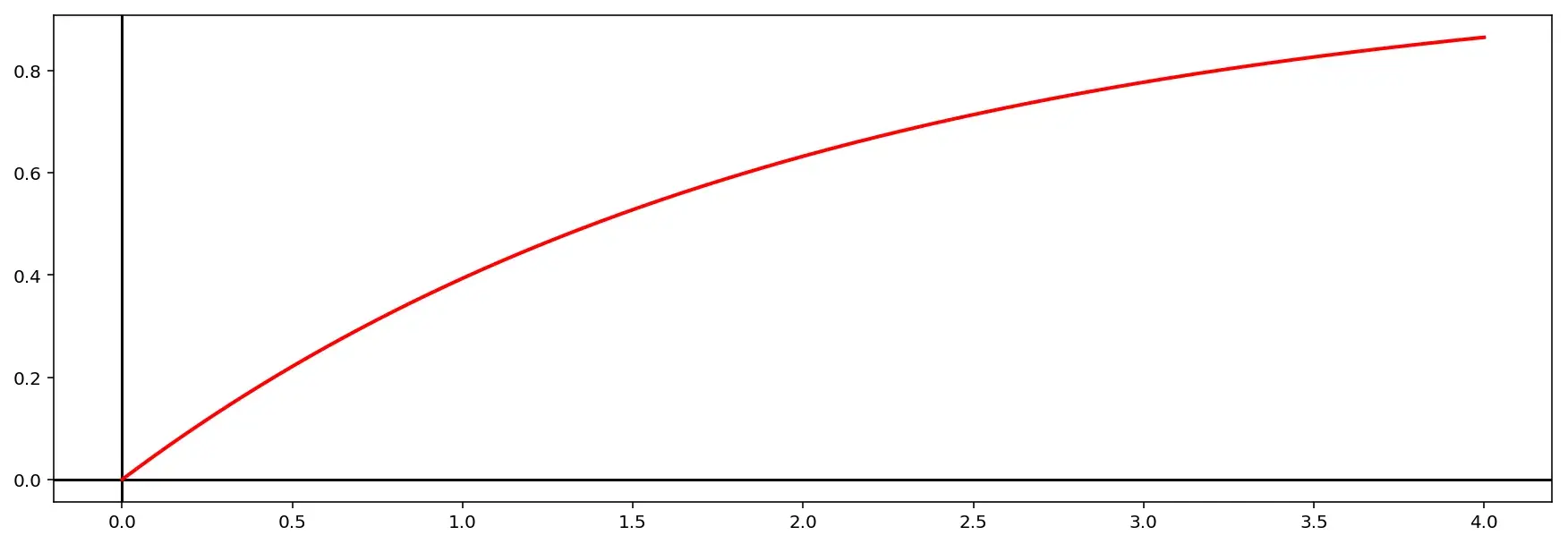
Для примера, можно поглядеть на плотность вероятности функции экспоненциального распределения. Формула самой функции выглядит так:
\[F(x)= \begin{cases} 1-e^{-\lambda x}, &x\ge 0 \\ 0, &x<0 \end{cases}\]график функции распределения при \(\lambda=0.5\):
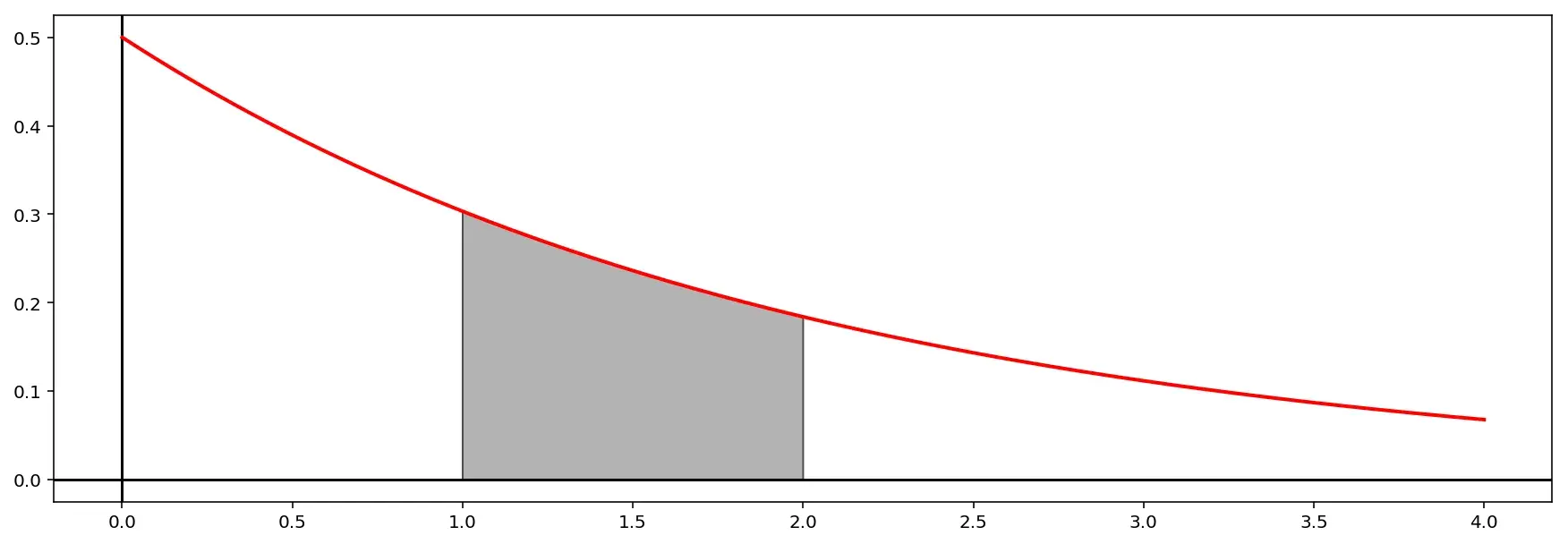
А вот так выглядит формула плотности распределения:
\[f(x)= \begin{cases} \lambda e^{-\lambda x}, &x\ge 0 \\ 0, &x<0 \end{cases}\]и ее график при \(\lambda=0.5\):
серым цветом на графике для примера показана вероятность того, что при \(\lambda=0.5\) \(X\) примет значение от 1 до 2, которую можно посчитать как:
\[P(1\le X\le 2)=\int_1^2\lambda e^{-\lambda x}dx \approx 0.239\]