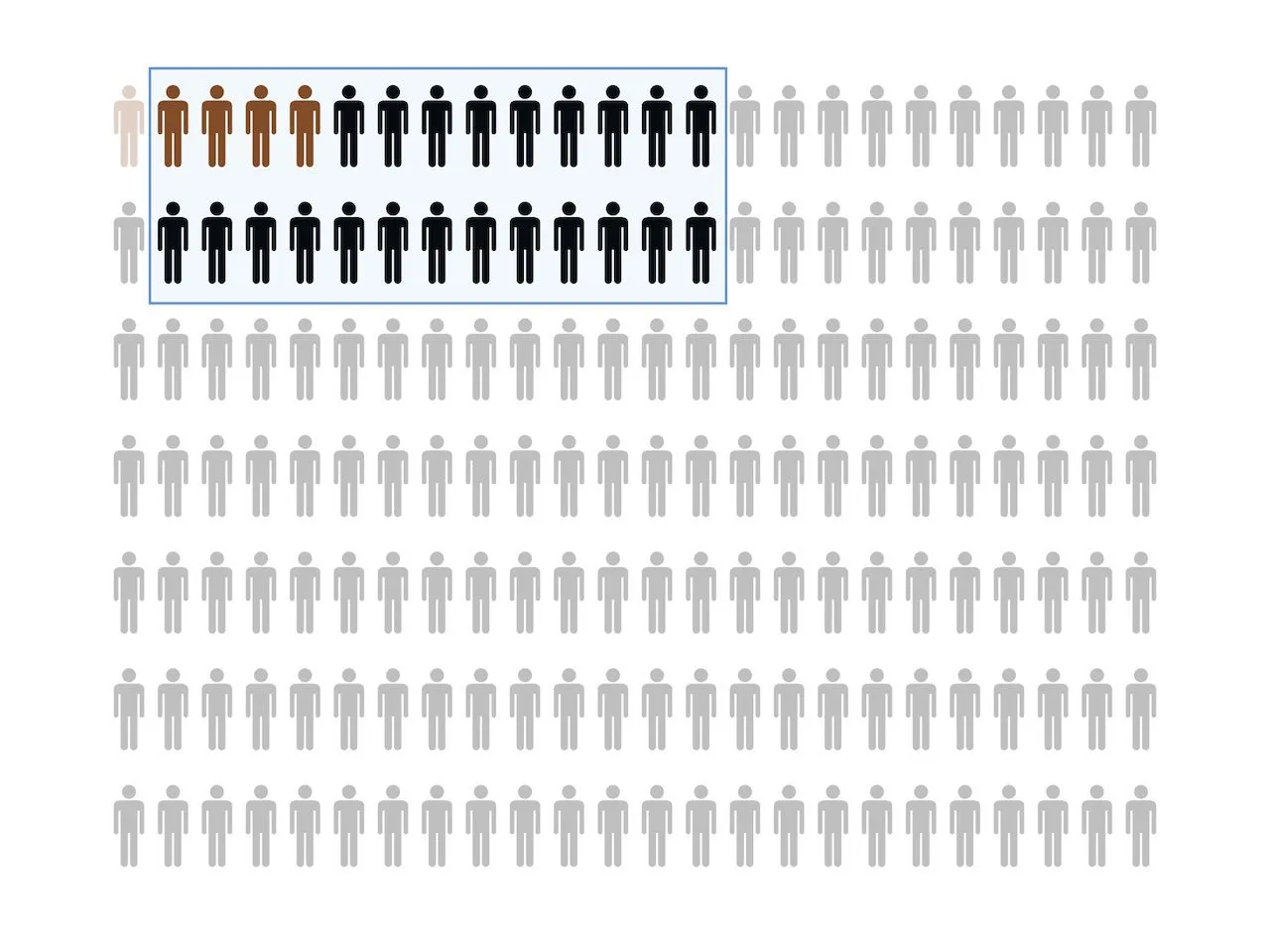Есть некое заболевание, про которое известно, что от него страдает 3% популяции. Существует тест, который с точностью 80% определяет, имеет человек это заболевание или нет, при этом тест в 13% случаев срабатывает ложно положительно, то есть, определяет заболевание у того, у кого его на самом деле нет.
Если тест показал, что у некоего человека есть заболевание, насколько вероятно, что этот человек реально болен?
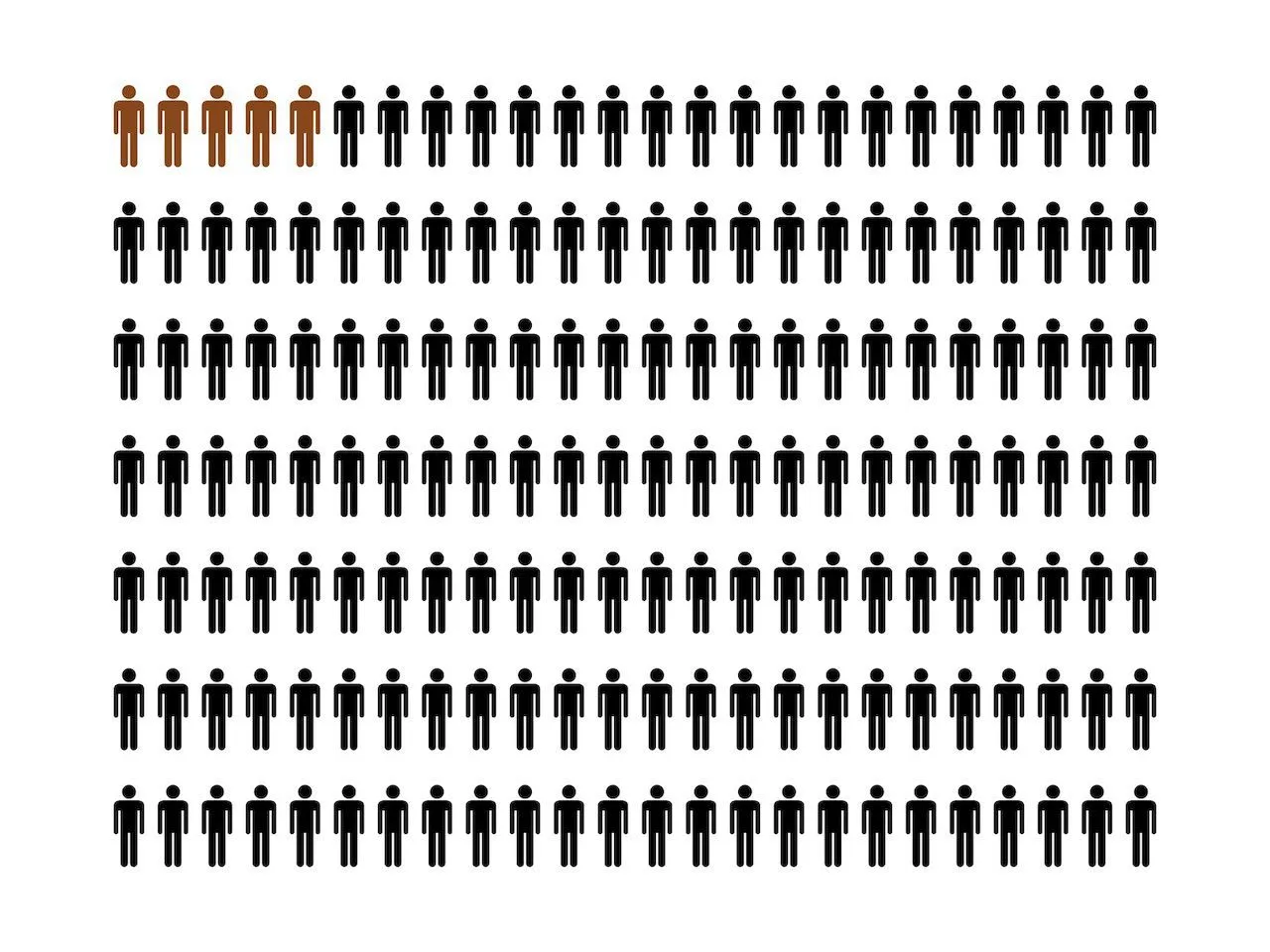
Ниже на иллюстрации выборка, в которой 3% людей, выделенных цветом, реально имеют заболевание, а 97% — нет:
Проводится тестирование, которое показывает, что некая часть людей из этой выборки имеет заболевание:
Так как тестирование с вероятностью 80% определяет заболевание, четверо из пяти реально заболевших были определены корректно. При этом, вместе с ними, положительный результат получила довольно большая группа не имеющих заболевание людей.
Вычислить вероятность, с которой человек был определён ложно положительно, можно по формуле:
\[\frac{P(\text{sick})}{P(\neg\text{sick})} \times \frac{P(+|\text{sick})}{P(\neg\text{sick}| +)} = \frac{P(\text{sick}|+)}{P(\neg\text{sick}|+)} \]Подставим в эту формулу реальные цифры с картинки выше. Из 175 человек 5 реально болеющих и 170 не болеющих; 4 из этих 5 болеющих корректно определяются тестированием, а 22 — ложно:
\[\frac{5/175}{170/175} \times \frac{4/5}{22/170} = \frac{4/26}{22/26}\approx 0.18\]Получается, что при этих исходных условиях, человек получивший положительный результат тестирования, с вероятностью всего 18% на самом деле болен.