Правдоподобием можно использовать для сравнения возможных значений параметра \(\pi\). Например, студент случайным образом отвечал на вопросы теста, подразумевающие ответ “да” или “нет”, и оказалось, что у него 8 правильных ответов из 10. Если он отвечал случайно, то параметр \(\pi\) должен был оказаться равен 0.5, однако данные говорят о том, что он равен 0.8. Насколько более вероятно, что студент отвечал неслучайно, то есть попал в точку в 80% случаев, по сравнению с альтернативной гипотезой, что студен всё-таки отвечал на вопросы случайно?
Для того, чтобы провести такое сравнение, можно посчитать отношение правдоподобий:
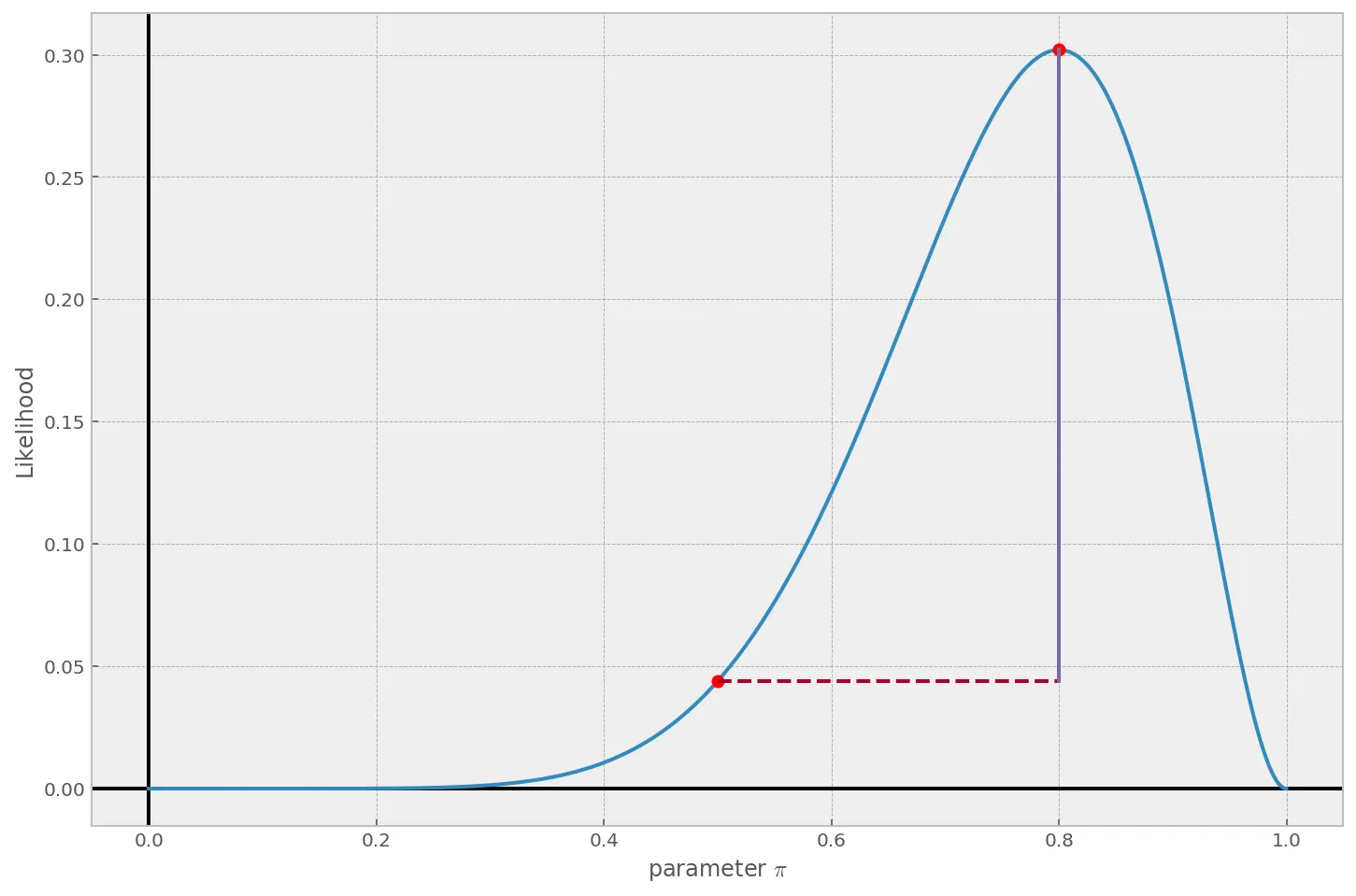
\[\frac{L(\pi = 0.8)}{L(\pi=0.5)}=\frac{0.302}{0.044}\approx 6.87\]На графике это выглядит так:
То есть, конкретно эти данные говорят о том, что гипотеза о неслучайном 80% попаданий в 6.87 раз более вероятна гипотезы случайного выбора.
Отношение правдоподобий можно посчитать для любых двух значений разных гипотез. Например, в случае 4 правильных ответов из 10 можно посчитать то же самое отношение гипотез 80% и 50%:
\[\frac{L(\pi = 0.5)}{L(\pi=0.8)}=\frac{0.205}{0.0055}\approx 37.25\]Для этих данных гипотеза о 50% в 37.25 раз более вероятна гипотезы о 80%.
Вот, как это выглядит на графике:
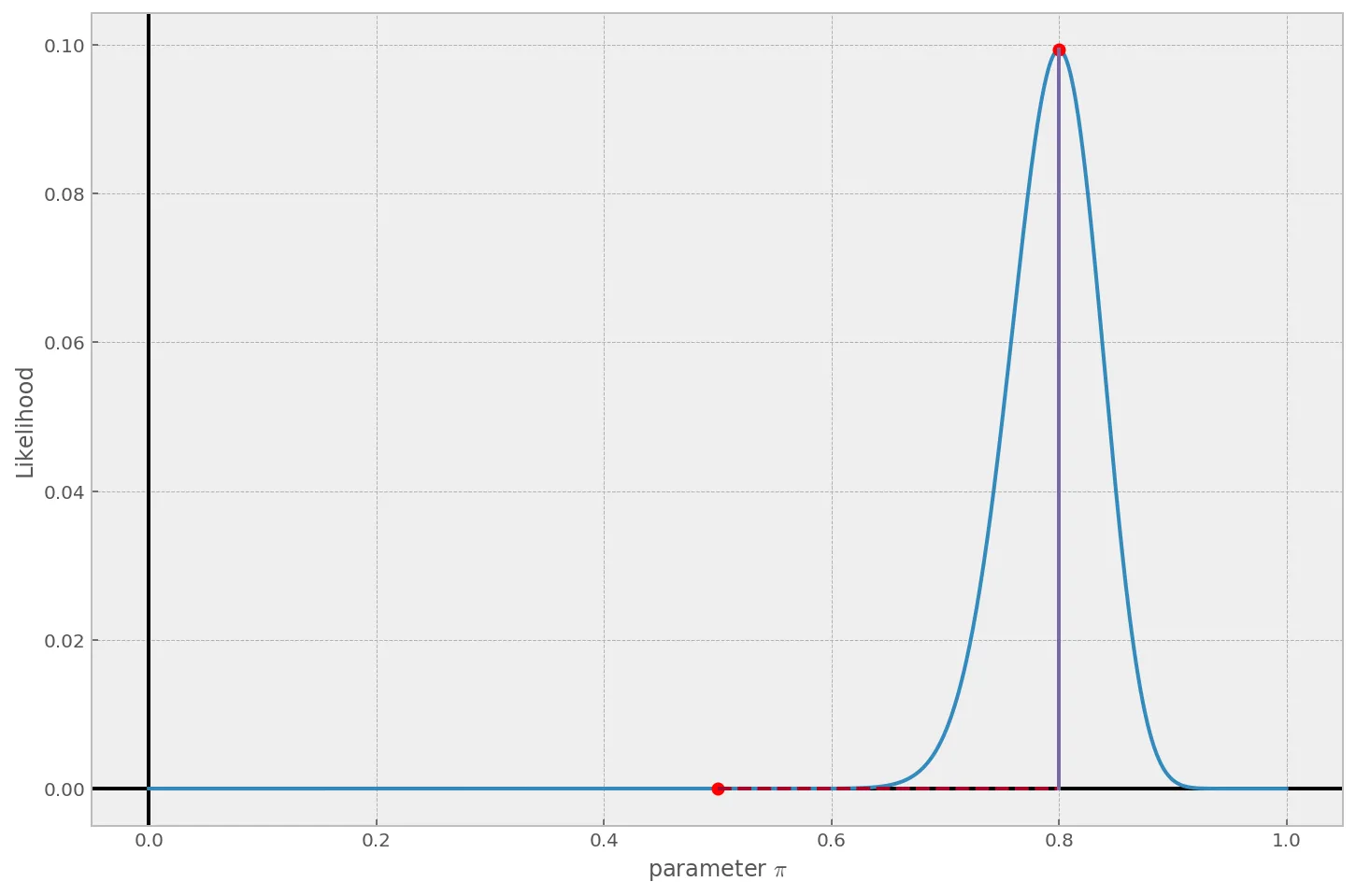
Если отношение равно 1, то обе гипотезы одинаково вероятны. Чем дальше значение оказывается от единицы, тем более вероятна одна из гипотез. Например, если в первом примере увеличить размер выборки в 10 раз, то есть, вопросов 100, а правильных ответов — 80, то отношение правдоподобий будет равно 234854258, что явно говорит о том, что гипотеза 80% гораздо более вероятна, чем гипотеза 50%:
\[\frac{L(\pi = 0.8)}{L(\pi=0.5)}=\frac{0.0993}{4.23 \times 10^{-10}}\approx 234854258\]График для этих данных выглядит вот так:
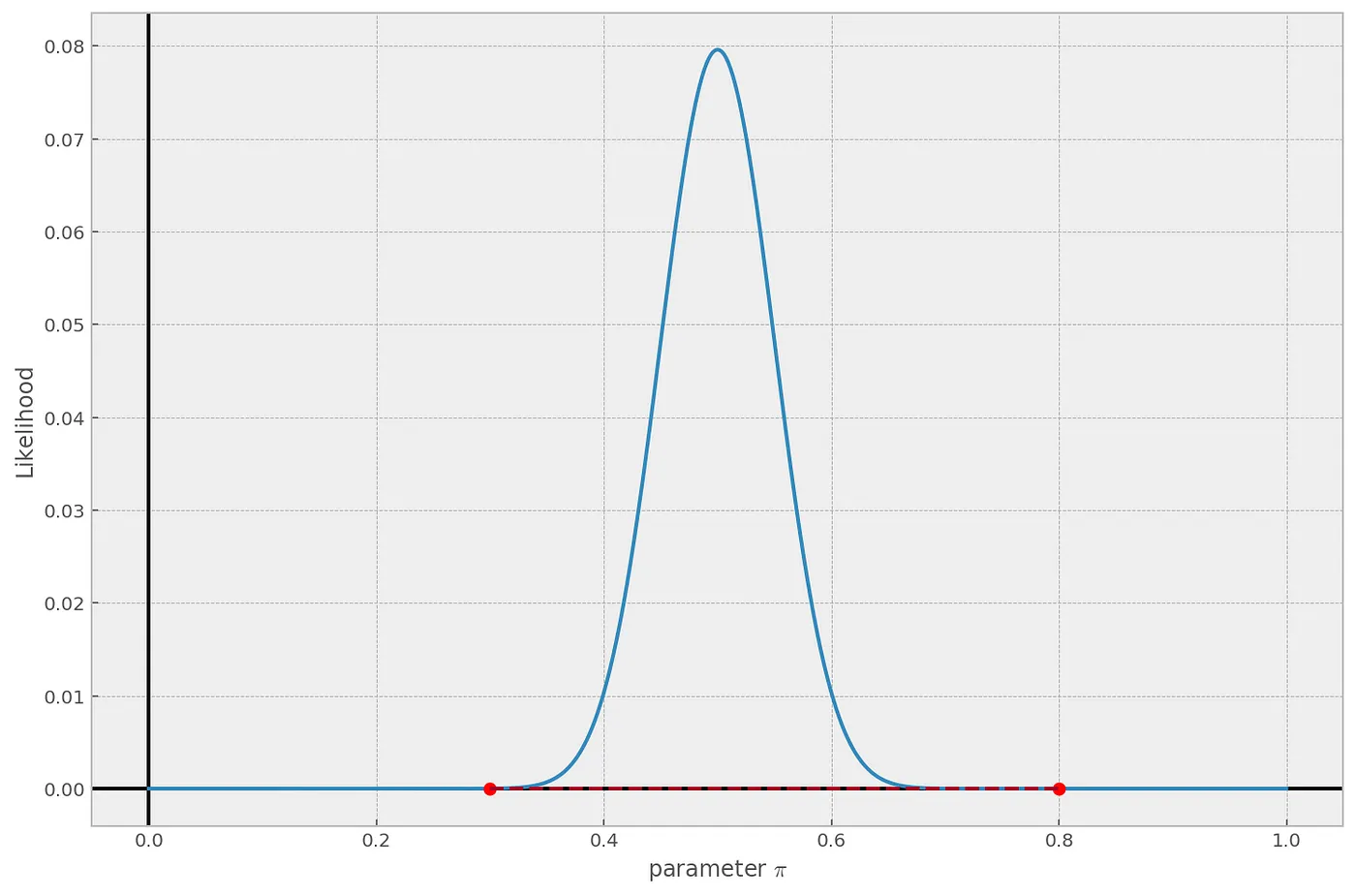
Конечно же, при вычислении отношения правдоподобий, стоит поглядеть на данные. Например, бросая монету 100 раз и, получив 50 орлов, можно, не зная, что максимальное правдоподобие достигается при 0.5, попытаться вычислить отношение правдоподобий при 0.8 и 0.3:
\[\frac{L(\pi = 0.8)}{L(\pi=0.3)}=\frac{1.3 \times 10^{-5}}{1.62 \times 10^{-11}}\approx 803463\]Огромная разница между 0.3 и 0.8 потверждает гипотезу, однако реальные данные говорят о том, что мы сравниваем незначимые значения, поскольку реальная вероятность для этих данных — 0.5: