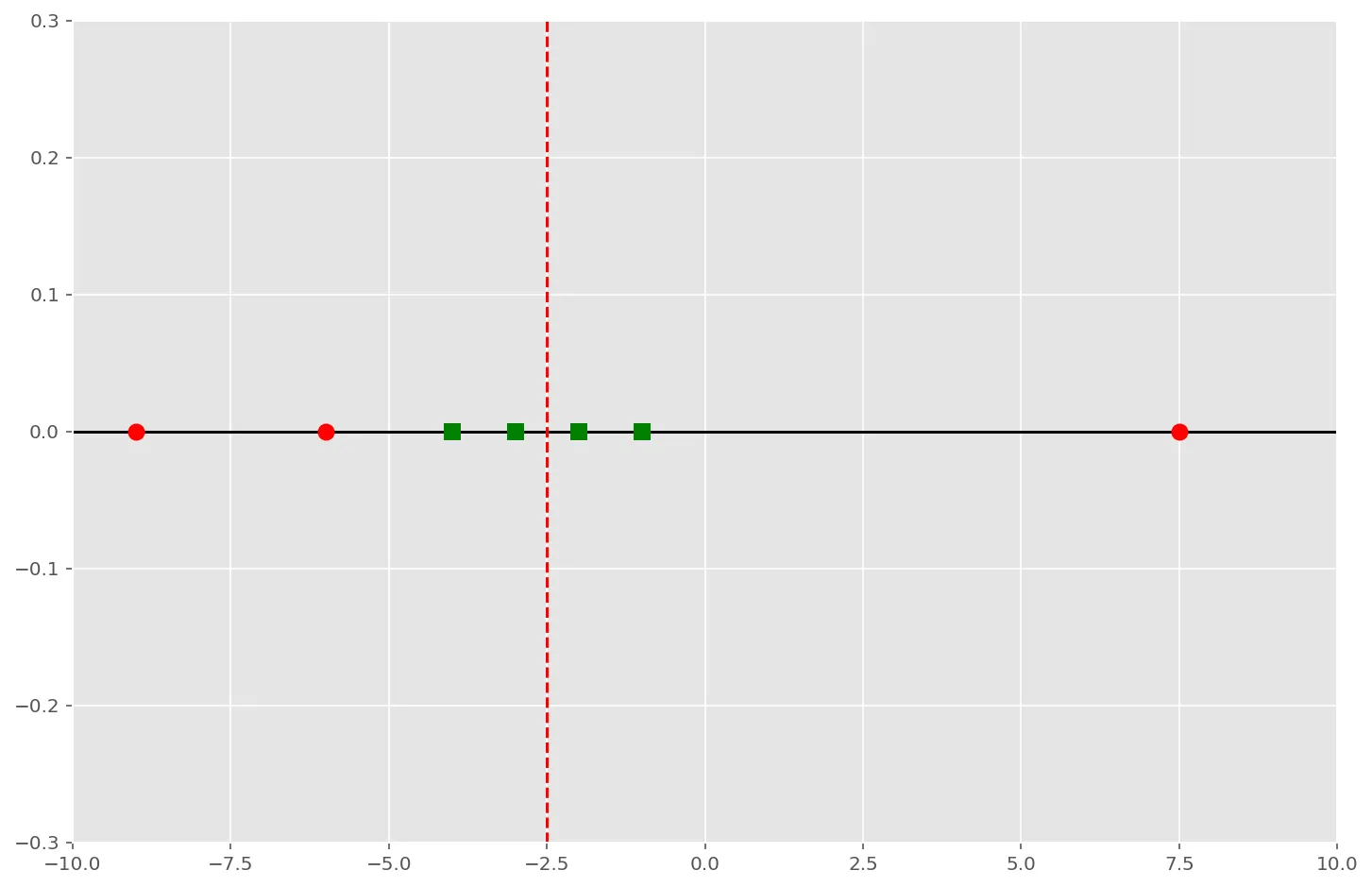
Допустим, у нас есть два игрушечных набора данных: [-9, -6, 7.5] и [-4, -3, -2, -1].
Как можно быстро и просто их сравнить? Первое, что приходит в голову: посчитать среднее значение для каждого набора:
\[\mu = \frac{1}{n}\sum_{i=1}^nx_i\]Что покажет это значение? Абсолютно ничего, поскольку у обоих наборов оно одинаково и равно -2.5.
Давайте отобразим наборы данных на графике и визуально оценим их:
Красные точки — это первый набор данных, зелёные квадраты — второй, а вертикальная красная пунктирная линия — среднее значение обоих наборов.
На графике явно видно, что данные обоих наборов совершенно по-разному разбросаны относительно среднего значения: зеленые квадраты сгруппированы тесно, а красные точки лежат довольно далеко. Вот эту разницу и призвана выразить в числах дисперсия, которая есть не что иное, как средний разброс величин относительно среднего значения набора данных:
\[Var(X) = \frac{1}{n}\sum_{i=1}^n(x_i - \mu)^2\]Простыми словами, для того, чтобы посчитать дисперсию, нужно вычесть из каждого элемента набора среднее значение и возвести эту разницу в квадрат. Затем нужно все полученные значения сложить и поделить сумму на количество элементов набора.
Посчитаем дисперсию для первого набора:
\[Var(x_1) = \frac{(-9+2.5)^2+(-6+2.5)^2+(7.5+2.5)^2}{3} = 51.5\]и для второго:
\[Var(x_2) = \frac{(-4+2.5)^2 + (-3+2.5)^2 + (-2+2.5)^2 + (-1+2.5)^2}{4} = 1.25\]Понятно, что для таких маленьких наборов данных дисперсию можно не считать, потому как совсем небольшие наборы можно оценить в уме, для наборов чуть больше — достаточно построить график, разница на котором будет видна невооружённым взглядом, а, вот, когда наборы большие, разброс бывает совершенно неочевиден и в этих случаях на помощь приходит мера дисперсии.