Аффинная комбинация — это такая линейная комбинация точек аффинного пространства, у которой общая сумма коэффициентов равна единице
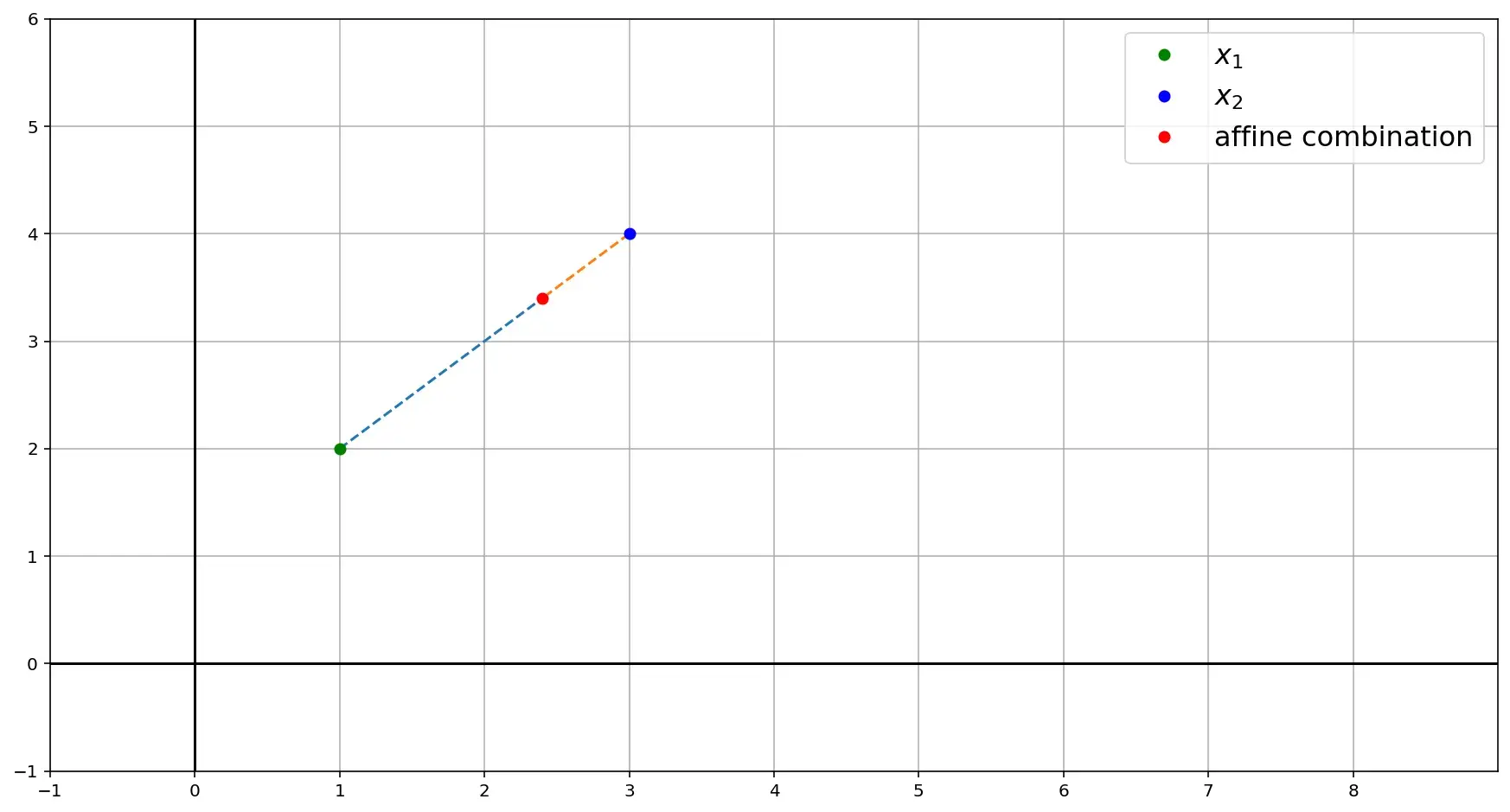
\[x = \theta_1 x_1+ \theta_2 x_2 + \ldots + \theta_k x_k, \sum_{i=1}^n \theta_i = 1\]Допустим, у нас есть две точки \(x_1\) с координатами \((1, 2)\) и \(x_2\) с координатами \((3, 4)\). Выберем для них коэффициенты \(\theta_1\) и \(\theta_2\) такие, чтобы их сумма была равна единице. Пусть это будет, например, 0.3 и 0.7. Тогда их аффинная комбинация равна
\[x = 0.3 x_1 + 0.7 x_2 = 0.3\binom{1}{3} + 0.7\binom{2}{4} = \binom{2.4}{3.4}\]Геометрически на плоскости такая аффинная комбинация будет выглядеть как точка, находящаяся на прямой, соединяющей \(x_1\) и \(x_2\)
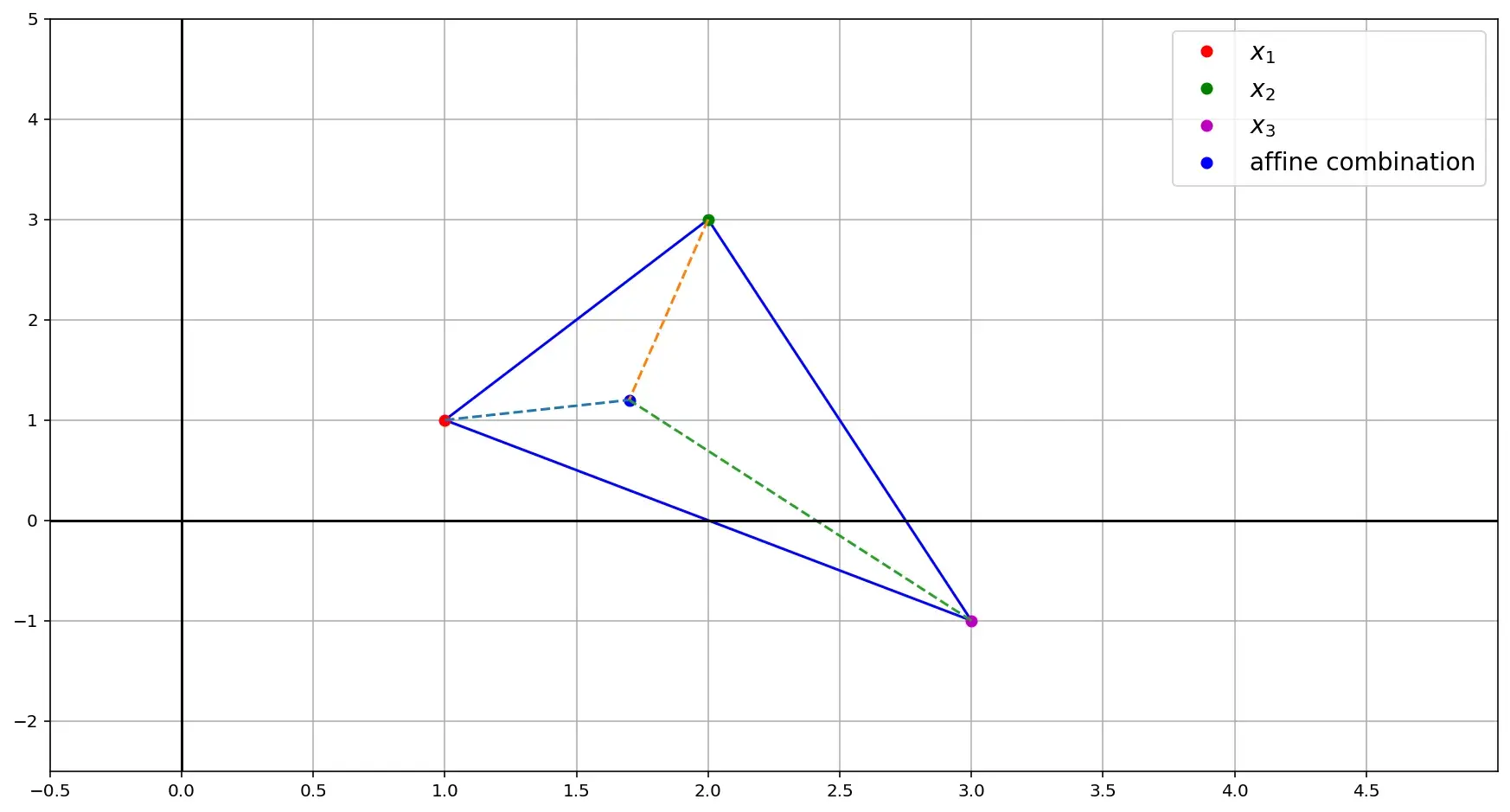
Для трех точек на плоскости аффинная комбинация попадет внутрь треугольника, образованного этими точками, в том случае, если все коэффициенты положительны.
Например, возьмем три точки \(x_1(1,1)\), \(x_2(2, 3)\) и \(x_3(3, -1)\). Возьмем коэффициенты 0.5, 0.3 и 0.2, соответственно:
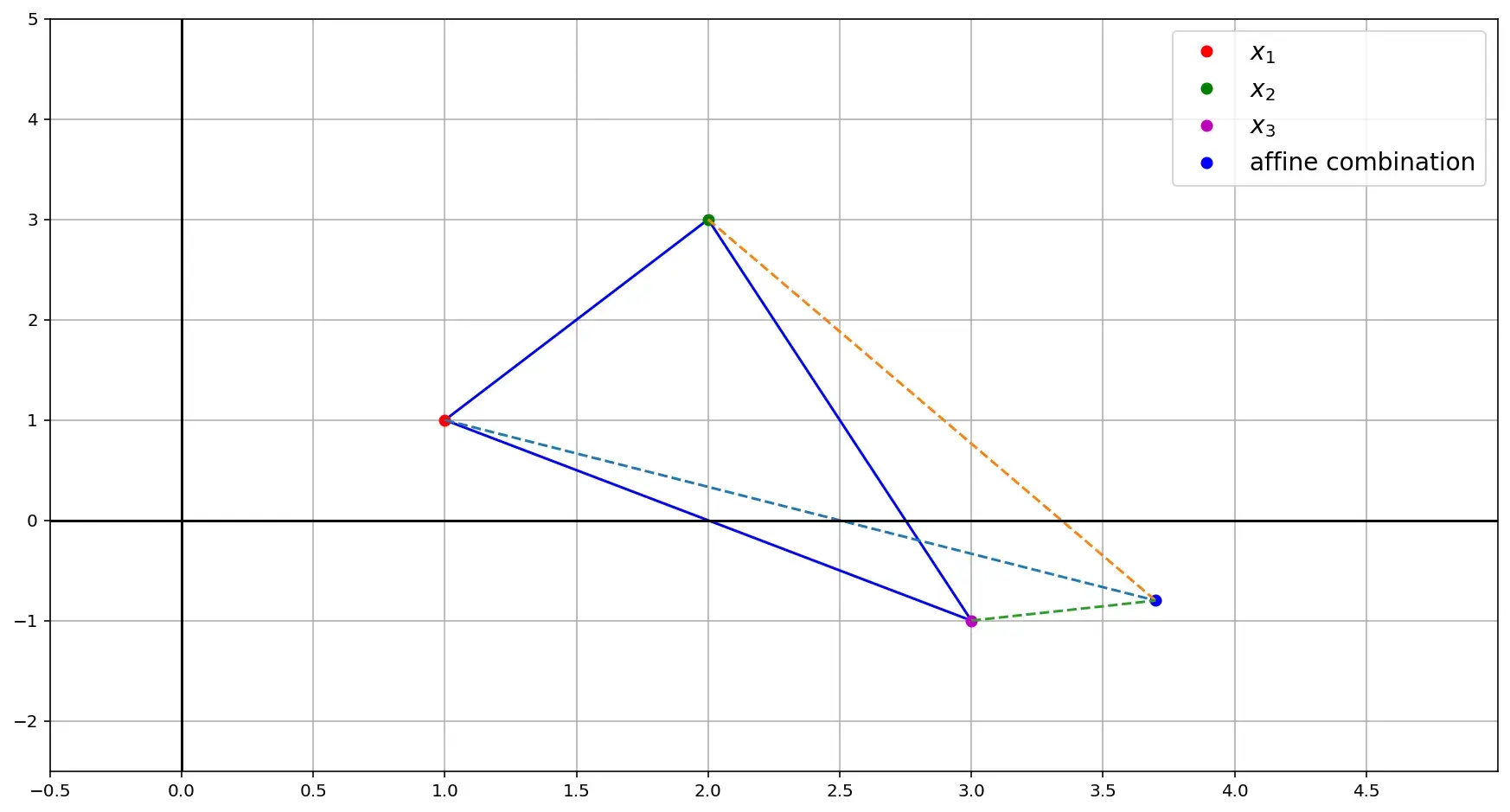
\[x=0.5\binom{1}{1} + 0.3\binom{2}{3} + 0.2\binom{3}{-1} = \binom{1.7}{1.2}\]Если взять какой-то коэффициент больше единицы, то аффинная комбинация окажется за пределами треугольника. Помните, что в сумме коэффициенты должны быть равны единице, поэтому для соблюдения этого условия какие-то коэффициенты придется сделать отрицательными. Оставим точки те же, что и в предыдущем примере, однако коэффициенты теперь возьмем -0.5, 0.3 и 1.2:
\[x=-0.5\binom{1}{1} + 0.3\binom{2}{3} + 1.2\binom{3}{-1} = \binom{3.7}{-0.8}\]в этом случае точка окажется снаружи треугольника: