теорема об аффинном множестве

Есть такая теорема об удивительном свойстве аффинного множества:

Пусть \(X\subseteq \mathbb{R}^n\) — аффинное множество. Тогда для любого \(x_0\) множество

\[L = X- x_0\]

это линейное подпространство. \(L\) — единственное и не зависит от выбора \(x_0\).

Другими словами, если у нас есть какое-то аффинное множество \(X\), то, если взять любую точку этого пространства, и вычесть поэлементно из всего множества, то в результате получится линейное подпространство \(L\). При этом неважно, какую точку в аффинном множестве вы выбираете, линейное подпространство будет всегда получаться одно и то же.

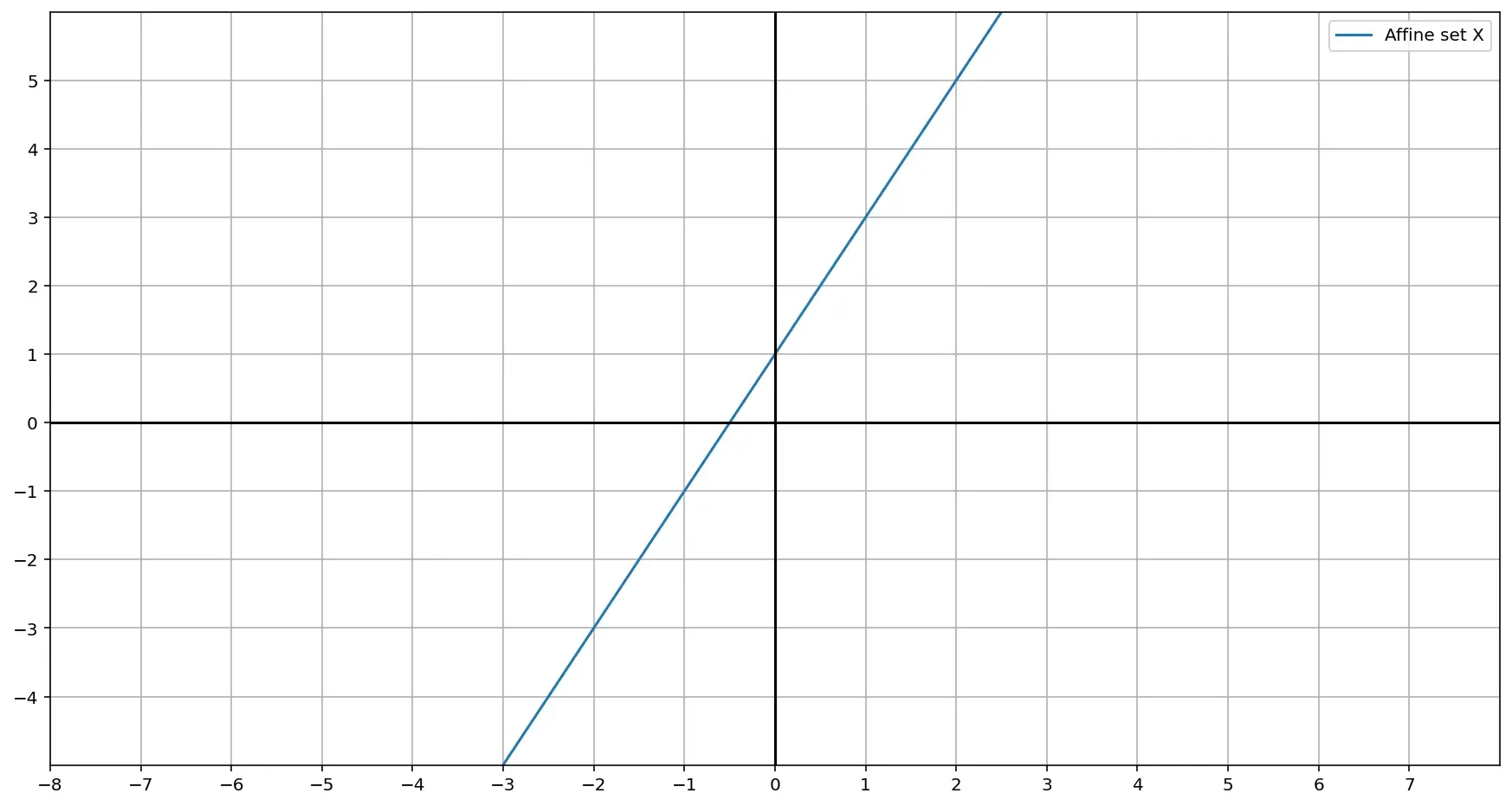
Рассмотрим такой пример. Допустим, у нас есть аффинное множество — прямая \(X\), которая задана уравнением \(y = 2x + 1\):

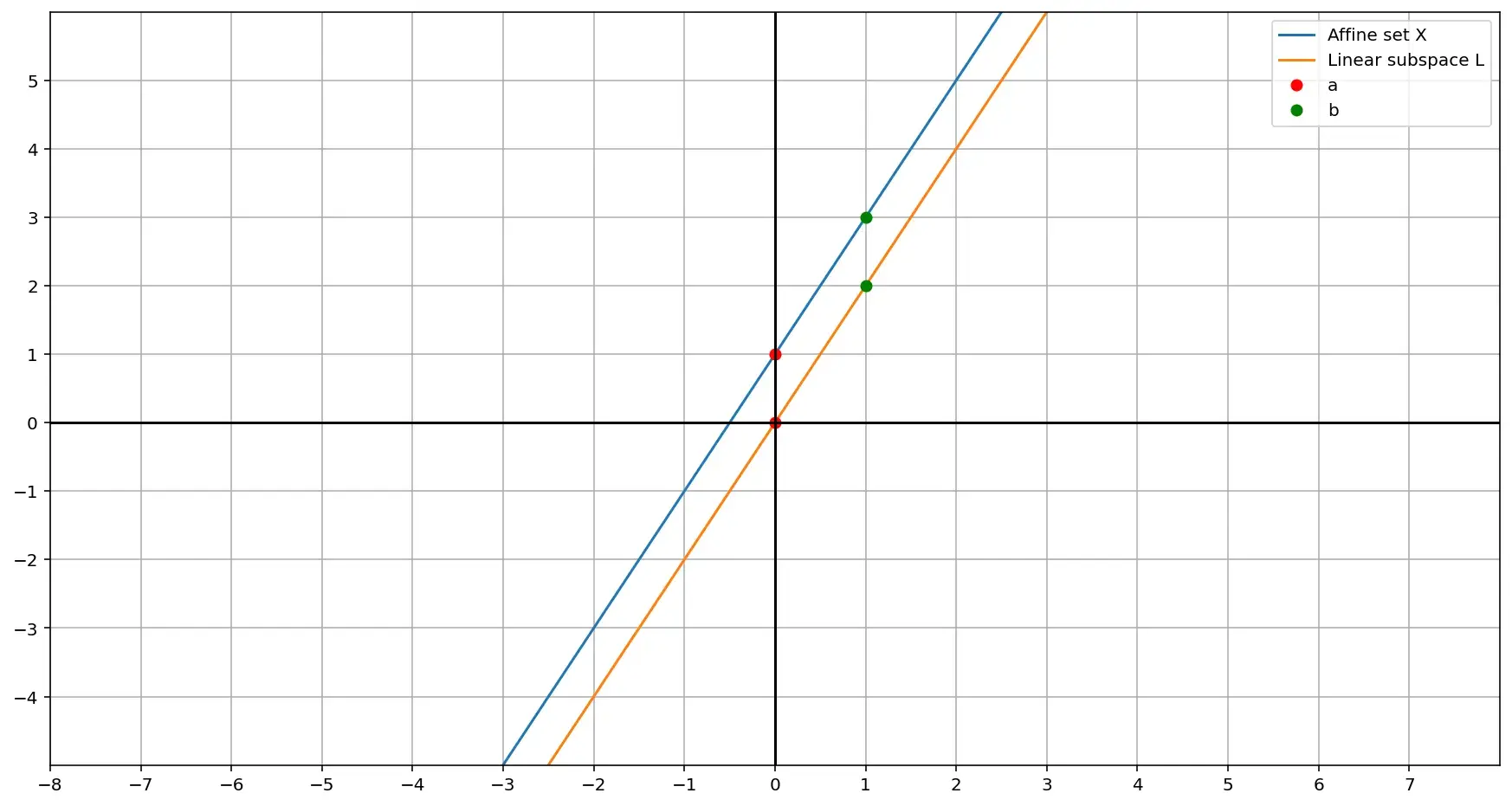
Если мы возьмем любую точку на этой прямой, например, \((0, 1)\) и вычтем из всего множества, то получим прямую, которая параллельна исходной прямой и проходит через начало координат \((0, 0)\).

Точка \(a (0, 1)\) из аффинного множества \(X\) станет точкой с координатами \((0, 0)\) в \(L\), а точка \(b (1, 3)\) — точкой с координатами \((1, 2)\):

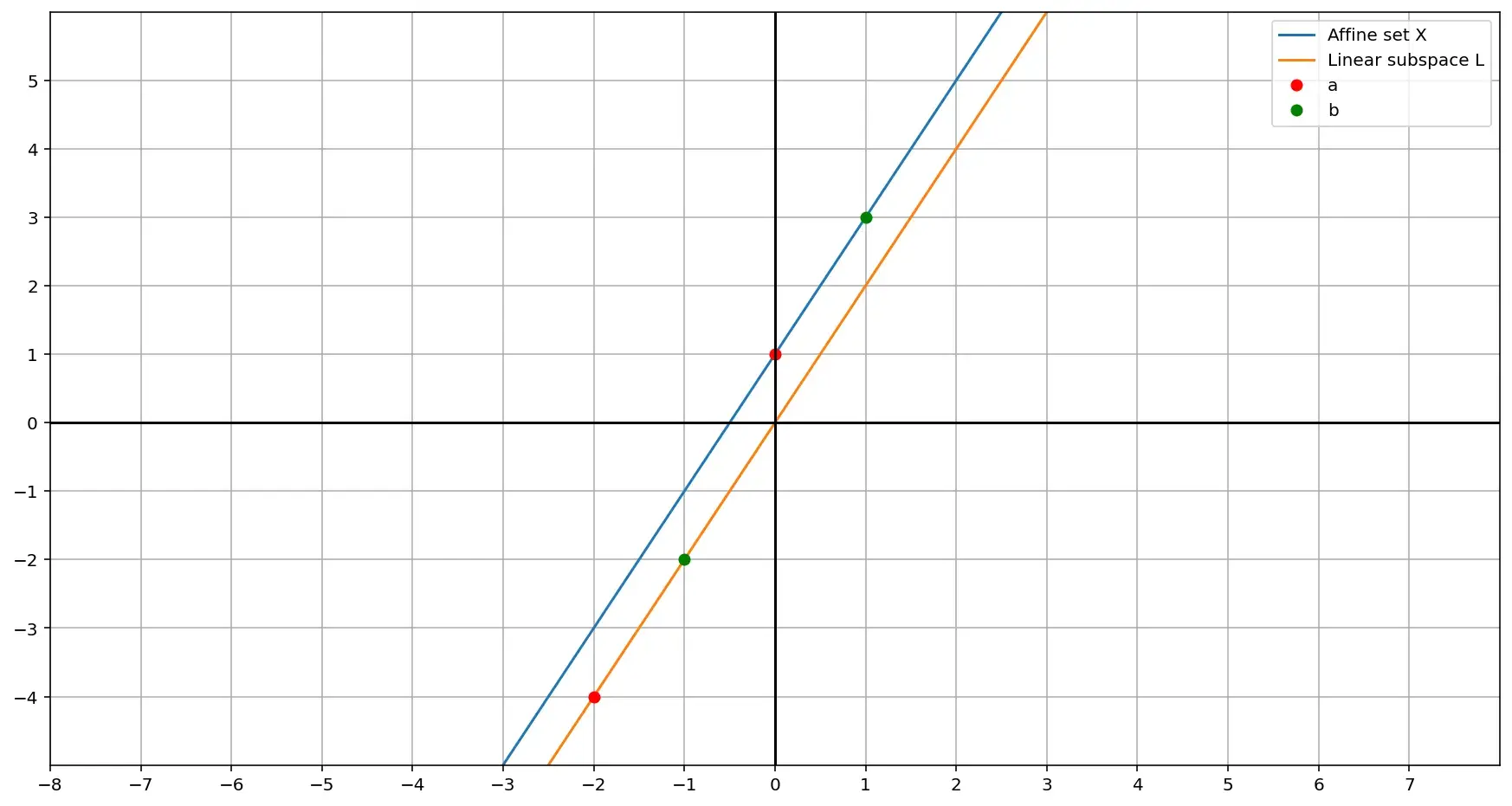
Теперь возьмем какую-нибудь другую точку, например \((2, 5)\) и вычтем ее из множества \(X\):

в этом случае точка \(a (0, 1)\) становится точкой с координатами \((-2, -4)\), а точка \(b\) получает координаты \((-1, -2)\). При этом линейное подпространство \(L\) чудесным образом остается тем же самым.