условная вероятность

Многие наверняка сталкивались с формулой вычисления условной вероятности, которая выглядит следующим образом:

\[P(A|B) = \frac{P(A,B)}{P(B)}\]

Вероятность события \(A\), при условии того, что произошло событие \(B\), равна отношению вероятности того, что произошли одновременного события \(A\) и \(B\) к вероятности того, что произошло событие \(B\).

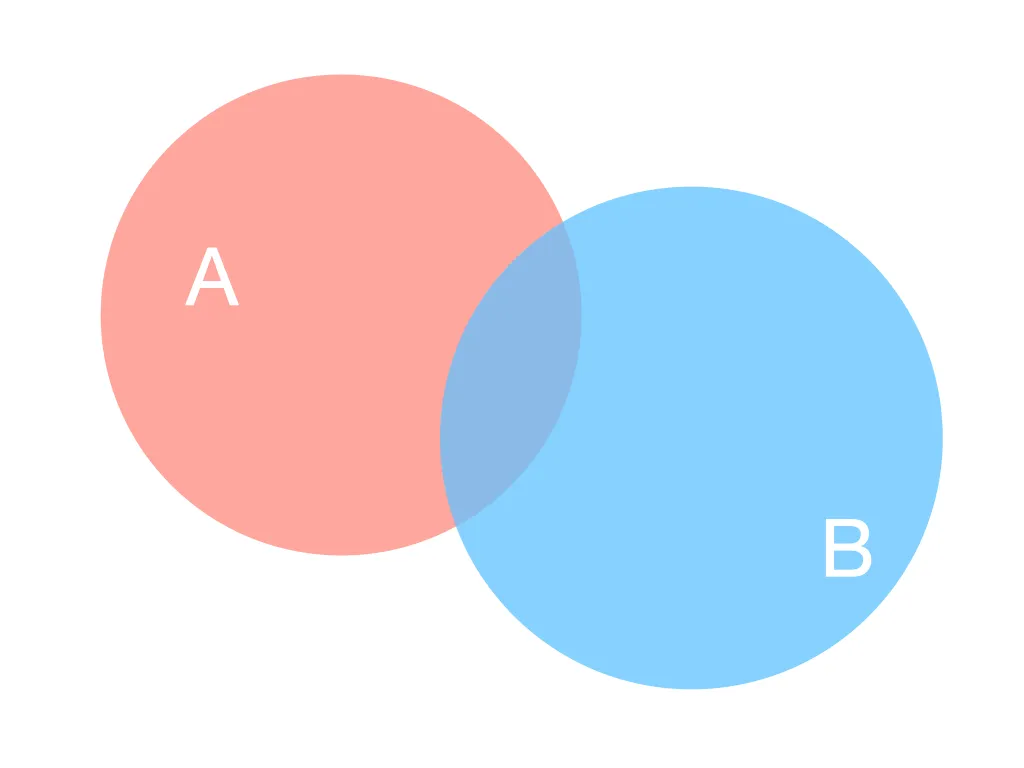
А теперь простая иллюстрация, которая поможет наглядно понять, откуда берется это отношение:

Событие \(A\) одновременно с событием \(B\) случается в том месте, где круги наложены друг на друга, размер этой части — это числитель.

Событие \(A\), при условии того, что произошло событие \(B\) — это просто отношение этой площади пересечения кругов, к общей площади круга \(B\). Простой пример. Допустим, откуда-то известно, что вероятность наступления события \(P(B) = 0.64\), а вероятность одновременного события \(P(A,B) = 0.08\), тогда вероятность \(P(A|B)\):

\[P(A|B) = \frac{P(A,B)}{P(B)} = \frac{0.08}{0.64}=0.125\]