Множество \(X\subseteq \mathbb{R}^n\) называется выпуклым, если вместе с любой парой точек \(x_1, x_2 \in X\)оно содержит все точки вида

\[x_\theta = \theta x_1 + (1-\theta)x_2\]

В этом месте выпуклое множество определяется точно также, как и аффинное, разница в ограничениях на коэффициент \(\theta\). Если у аффинного множества коэффициент может быть любым действительным числом, то у выпуклого множества ограничение \(\theta \in [0,1]\).

Это означает, что выпуклое множество можно определить как множество, в котором для каждых двух любых точек содержится и весь отрезок, их соединяющий.

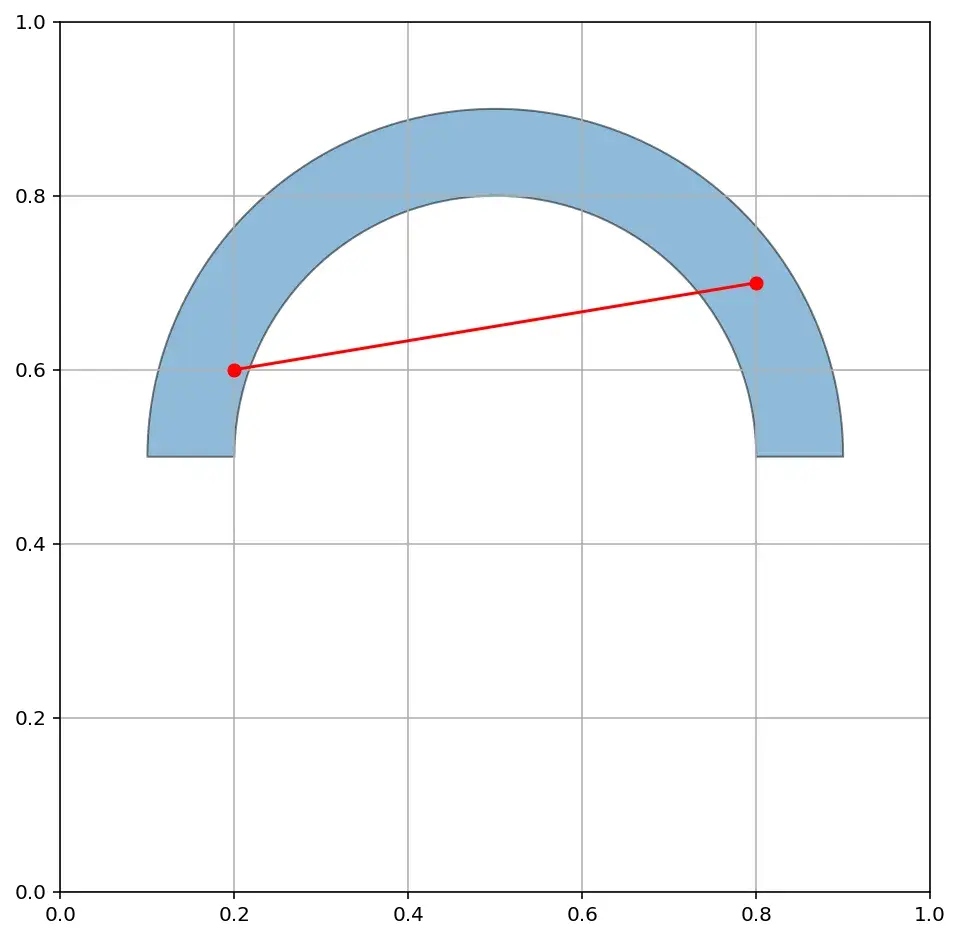
Вот такое множество — невыпуклое, потому что оно содержит такие пары точек, для которых отрезок, их соединяющий, окажется вне множества:

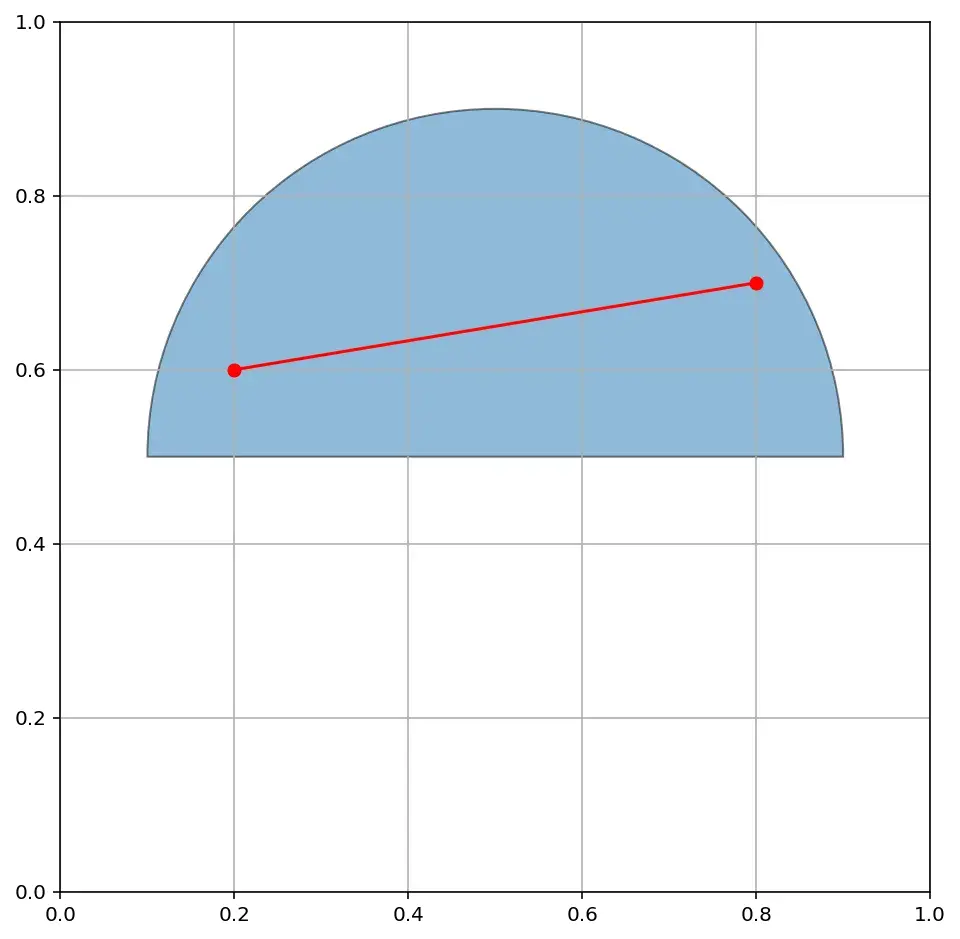
А вот такое, напротив, выпуклое, потому что все пары точек вместе с отрезками живут в этом множестве:

Примерами выпуклых множеств могут служить:

  • любое аффинное множество

  • луч, отрезок

  • шар по норме в \(\mathbb{R}^n\)

\[\{x \in \mathbb{R}^n \big| \|x - x_c\|\le r \}\]
  • эллипсоид
\[\mathcal{E}(x_c,P) = \{x\in \mathbb{R}^n\big| (x-x_c)^TP^{-1}(x-x_c)\le 1 \}\]

где \(P\) — это симметричная положительно определенная матрица

\[P = P^T \succ 0\]
  • решение системы линейных неравенств
\[x\in \mathbb{R}^n \big| Ax\le b, b\in \mathbb{R}^{m\times n}, b\in \mathbb{R}^n\]
  • гиперплоскость
\[x\in \mathbb{R}^n \big| a^Tx = b, a\ne 0\]
  • полупространство
\[x\in \mathbb{R}^n \big| a^Tx \le b, a\ne 0\]
  • полиэдр (многогранник)
\[x\in \mathbb{R}^n \big| a^Tx \preccurlyeq b, Cx=d\]