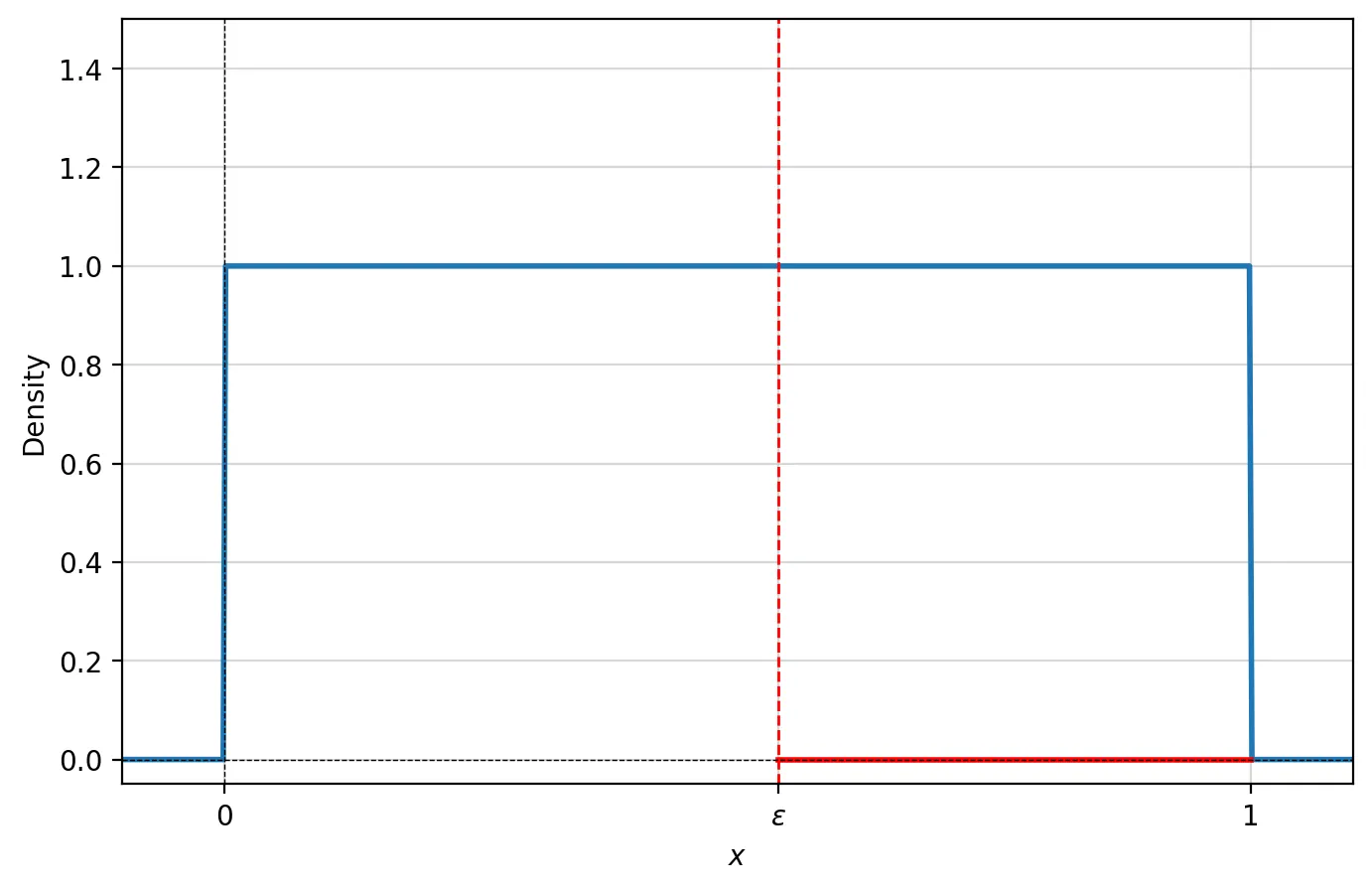
Пусть заданы случайные независимые, одинаково распределенные случайные величины \(X_i\), имеющие равномерное распределение на интервале \([0,1]\):
\[X_i \sim U(0,1)\]Рассмотрим связанную случайную величину \(Y_n\), которая представляет собой минимум из первых \(n\) элементов \(X_i\):
\[Y_n = \min\{X_1, \ldots, X_n\}\]Нас будет интересовать, как ведет себя \(Y_n\) при увеличении числа \(n\), и в частности, будет ли \(Y_n\) стремиться к нулю?
Если мы добавляем элементы из \(X_i\) в случайную величину \(Y_n\), то значения, оказавшиеся больше уже найденного минимума, никак не повлияют на \(Y_n\). Только те значения, которые меньше найденного минимума, повлияют на значение \(Y_n\), уменьшив его. То есть значение \(Y_n\) можно либо оставить прежним, либо уменьшить.
Так как такая случайная величина может только уменьшаться, то верно неравенство:
\[Y_{n+1}\le Y_n\]По мере увеличения значения \(n\) можно ожидать, что \(Y_n\) будет приближаться к нулю, поэтому можно сделать предположение, что при достаточно больших \(n\) случайная величина \(Y_n\) сходится к нулю.
Для проверки предположения зафиксируем некоторое положительное значение \(\varepsilon\) и посмотрим на вероятность того, что расстояние между случайной переменной \(Y_n\) и нулем будет больше или равно \(\varepsilon\).
\[P(|Y_n-0|\ge \varepsilon\]Поскольку по условию задачи случайная величина \(Y_n\ge 0\) всегда, то \(|Y_n — 0| \ge \varepsilon\) эквивалентно \(Y_n \ge \varepsilon\):
\[P(|Y_n-0|\ge \varepsilon = P(Y_n\ge \varepsilon)\]Если \(\varepsilon > 1\) то, эта вероятность будет равна нулю, так как по определению у нас задано распределение на \([0,1]\), соответственно, не существует исходов, при которых \(Y_n\) окажется больше \(\varepsilon\). В этом случае:
\[ P(Y_n\ge \varepsilon) = 0\]Рассмотрим случай, при котором \(\varepsilon \le 1\). В этом случае минимум примет значение как минимум \(\varepsilon\) в том и только в том случае, когда все случайные переменные как минимум равны \(\varepsilon\):
\[P(Y_n\ge \varepsilon) = P(X_1\ge\varepsilon, \ldots, X_n\ge\varepsilon\]так как случайные величины независимы, то эта вероятность представляет собой произведение вероятностей того, что каждая из случайных величин примет как минимум значение \(\varepsilon\):
\[P(X_1\ge\varepsilon)\cdot \ldots \cdot P(X_n\ge\varepsilon)\]Вероятность того, что случайная величина примет значение больше или равное \(\varepsilon\) будет равна \((1 - \varepsilon)\). Так как случайная величина одинаково распределена все вероятности будут одинаковыми, поэтому получаем, что вероятность будет равна:
\[P(X_n\ge\varepsilon) = (1-\varepsilon)^n\]\(\varepsilon\) — неотрицательное число, \((1 - \varepsilon)\) строго меньше единицы. Если при \(n\) стремящемся к бесконечности, берем степень числа, меньше единицы, то значение будет сходиться к нулю:
\[(1-\varepsilon)^n\xrightarrow[n\to\infty]{}0\]При фиксированном \(\varepsilon > 0\) каждый \(X_i\) с вероятностью \((1 - \varepsilon)\) находится на интервале \([\varepsilon, 1]\). Чтобы минимум был не меньше \(\varepsilon\), все \(n\) значений должны попасть в этот интервал, что с ростом \(n\) становится все менее вероятным.
Отсюда можно сделать вывод, что случайная величина \(Y_n\) по вероятности сходится к нулю:
\[Y_n\xrightarrow[n\to\infty]{P}0\]