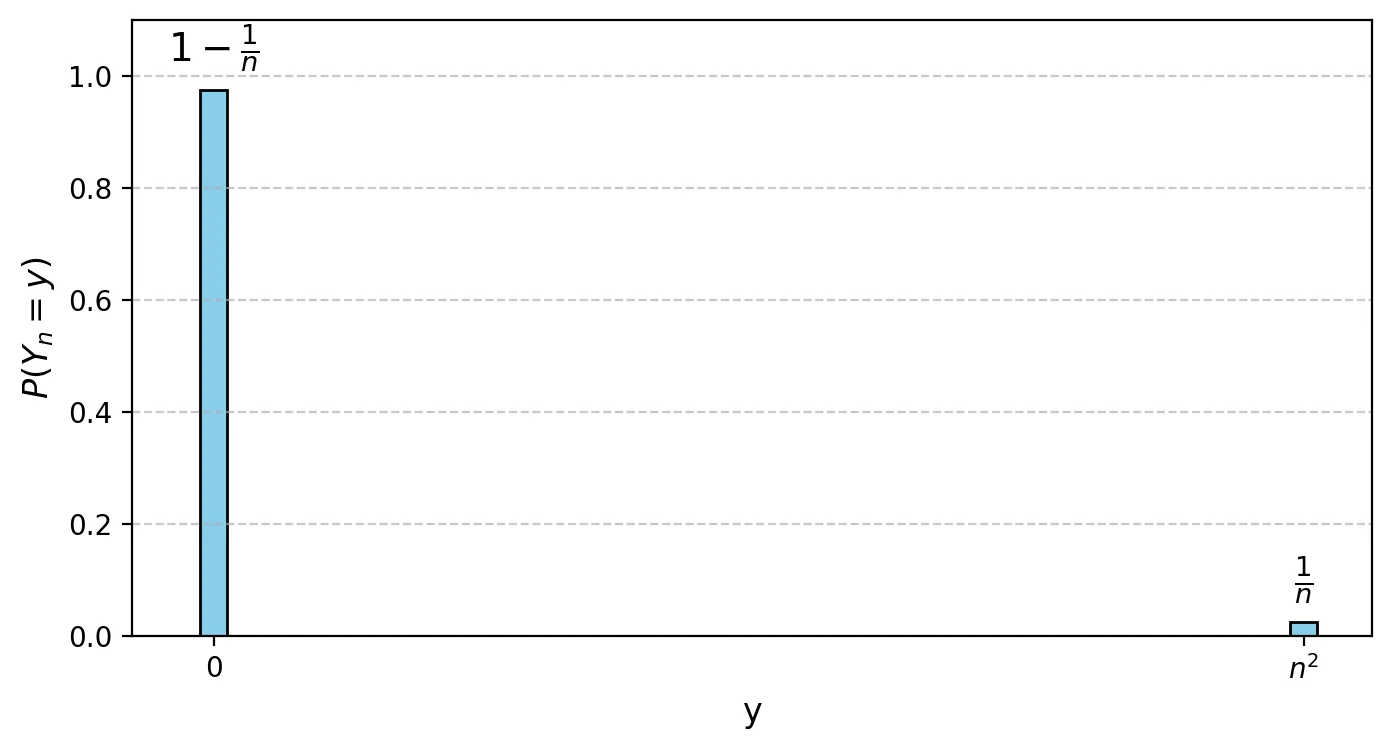В этой статье мы рассмотрим хороший пример, иллюстрирующий утверждение, что сходимость случайной величины по вероятности не означает сходимости ее матожидания.
Пусть задана случайная величина \(Y\), которая с вероятностью \(1–1/n\) принимает значение \(\theta\), и с вероятностью \(1/n\) принимает значение \(n^2\).
Логично будет предположить, что с ростом \(n\) эта случайная величина будет все чаще получать значение 0. При больших значениях \(n\) вероятность того, что \(Y_n\) примет большое значение \(n^2\), становится очень малой, а основной вклад дается нулевым значением. Другими словами, эта случайная величина сходится по вероятности к нулю.
Последовательность случайных величин сходится к некоторому значению \(\xi\) тогда и только тогда, когда при \(n\) стремящемся к бесконечности для любого положительного ε вероятность того, что значение случайной величины отклоняется от \(\xi\) больше, чем на \(\varepsilon\) равна нулю:
\[Y_n \xrightarrow[n\to\infty]{P}\xi \Leftrightarrow \forall \varepsilon> 0: \lim_{n\to\infty}P(|Y_n-\xi|\ge\varepsilon)=0 \]Возьмем и зафиксируем некоторое положительное значение \(\varepsilon > 0\). Поскольку случайная величина \(Y_n\) может принимать только два значения — 0 и \(n^2\), — при достаточно большом значении \(n\) число \(n^2\) будет существенно превосходить любое фиксированное \(\varepsilon\). Поэтому, если неравенство \(|Y_n - 0| \ge\varepsilon\) верно, то \(Y_n\) никак не может быть равно нулю, то есть это неравенство эквивалентно событию \(Y_n = n^2\). Однако, вероятность такого события равна \(1/n\), которая стремится к нулю с ростом значения \(n\):
\[P(|Y_n-0| \ge \varepsilon) = \frac{1}{n} \xrightarrow[n\to\infty]{}0\]Другими словами, с ростом \(n\) вероятность того, что \(Y_n\) отклонится от нуля более, чем на фиксированное значение \(\varepsilon\), становится пренебрежимо малой, что и означает сходимость \(Y_n\) по вероятности к нулю:
\[Y_n\xrightarrow[n\to\infty]{P}0\]Теперь поглядим, как себя ведет математическое ожидание этой случайной величины. Математическое ожидание случайной величины — это сумма всех ее возможных значений, умноженных на вероятность каждого из них:
\[\mathbb{E}[Y_n]=\sum_{y}y\cdot P(Y_n-y)\]где y пробегает все возможные значения случайной величины.
В нашем случае случайная величина \(Y_n\) принимает два значения:
- \(Y_n = n^2\) с вероятностью \(P(Y_n = n^2) = 1/n\)
- \(Y_n = 0\) с вероятностью \(P(Y_n = 0) = 1-1/n\)
Подставим эти значения в формулу матожидания:
\[\mathbb{E}[Y_n]=n^2\cdot\frac{1}{n}+0\cdot\bigg(1-\frac{1}{n}\bigg)=n^2 \cdot \frac{1}{n} = n\]Получаем, что матожидание случайной величины \(Y_n\) равно \(n\) и стремится к бесконечности при росте \(n\):
\[\mathbb{E}[Y_n] = n\xrightarrow{}[n\to\infty]\infty\]Это наглядно иллюстрирует ситуацию, когда случайная величина почти всегда близка к нулю, но изредка может принимать настолько большое значение, что оно вносит гигантский вклад в математическое ожидание.
Мы рассмотрели простой пример, показывающий, что если последовательность случайных величин сходится по вероятности к какому-то значению, то их математическое ожидание может не только не стремиться к этому значению, но и расходиться.