Распределение, состоящее из бинарных данных, то есть из таких объектов, которые можно отнести к одной из двух определённых категорий, называется биномиальным или распределением Бернулли. Для категорий часто можно встретить названия “успех” и “неудача”.
Такое распределение можно получить, если, например, подбрасывать монету и фиксировать результат каждого эксперимента. На выходе получится выборка, состоящая из бинарных данных, — “орёл” или “решка”.
Вот так выглядит формула вероятности определённого исхода y для выборки \(Y\), вероятность успеха в каждом отдельном эксперименте обозначен как переменная \(\pi\), а количество попыток — \(n\):
\[P(y) = \frac{n!}{y!(n-y)!}\pi^y (1-\pi)^{\pi-y}\]Чтобы стало понятно, рассмотрим такой пример. Я подхожу к одноподъездному высотному дому, на каждом этаже которого пять квартир. В этом доме живёт десять моих знакомых. У меня есть информация о том, на каких этажах эти знакомые живут, но я не знаю номеров квартир. Какова вероятность того, что позвонив всего в одну случайную квартиру на каждом из этих десяти этажей, я ни разу не попаду в квартиру знакомого?
Итак, количество попыток равно 10, поэтому \(n = 10\). Вероятность успеха при каждой попытке равна \(1/5\), поэтому \(\pi = 0.2\):
\[P(0) = \frac{10!}{0!\cdot 10!}(0.2)^0(0.8)^{10}\approx 0.107\]То есть, с вероятностью около 10.7% ни в одной из квартир не окажется моих знакомых.
Как насчет того, что хотя бы в одной из десяти квартир окажется знакомый?
\[P(1) = \frac{10!}{1!\cdot 10!}(0.2)^1(0.8)^9\approx 0.268\]Вероятность попасть хотя бы к одному знакомому оказывается равна 26.8%.
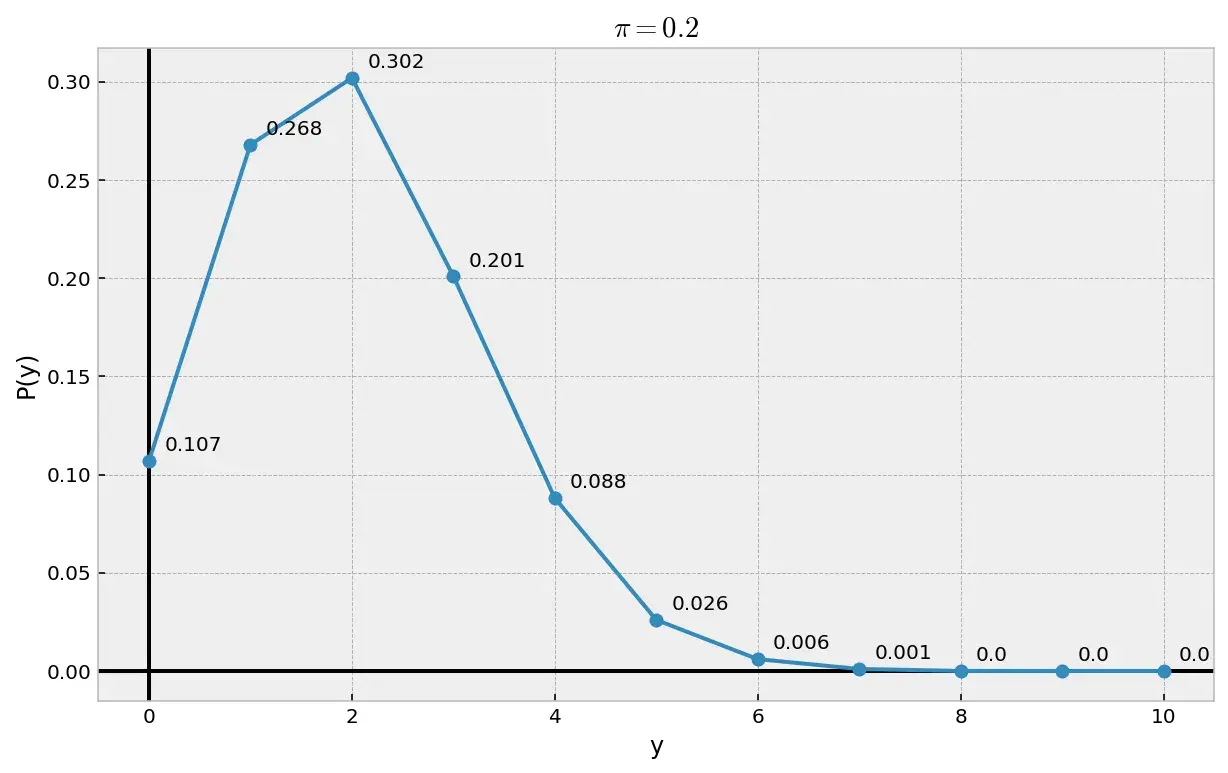
Вот так выглядит распределение вероятностей \(P(y)\) для значений y от нуля до десяти:
Как видно на графике, максимальная вероятность 30.2% встретить двух знакомых и нулевая — встретить восемь или больше.
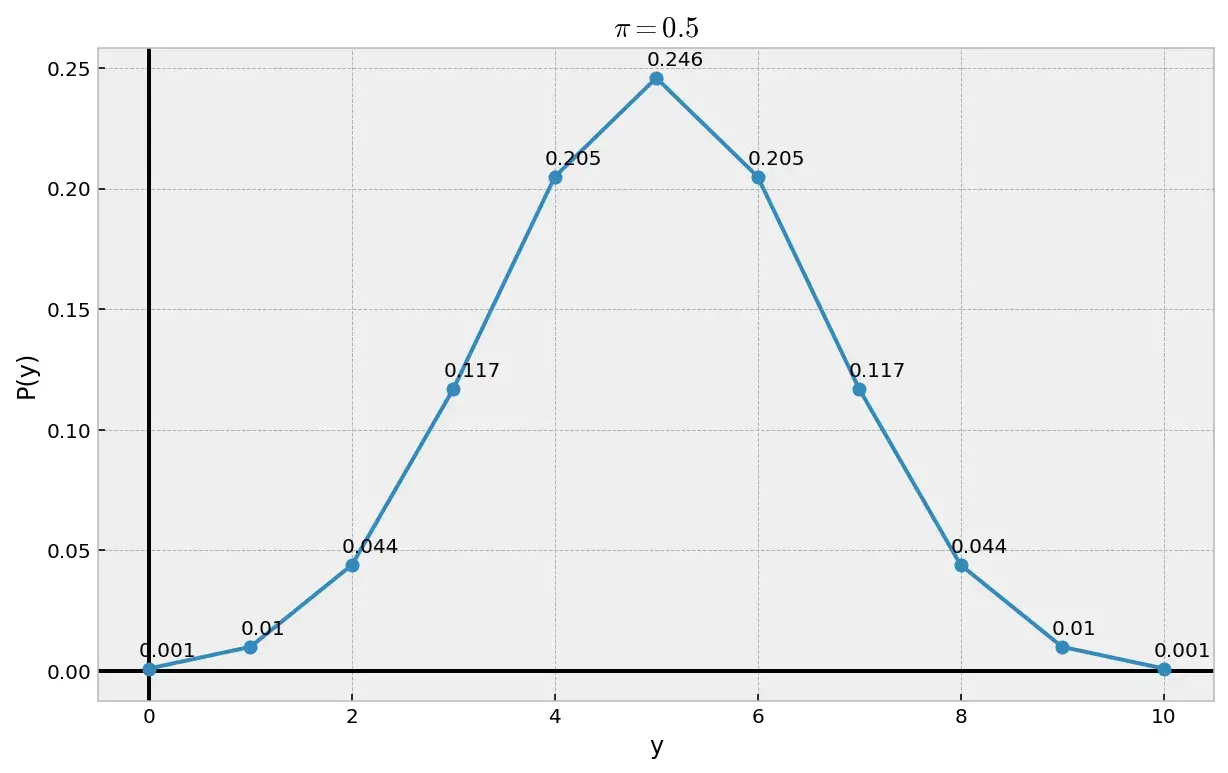
А вот как будет выглядеть график распределения вероятностей, если параметр \(\pi\) будет равен 0.5:
Распределение в этом случае становится симметричным и похожим на нормальное.
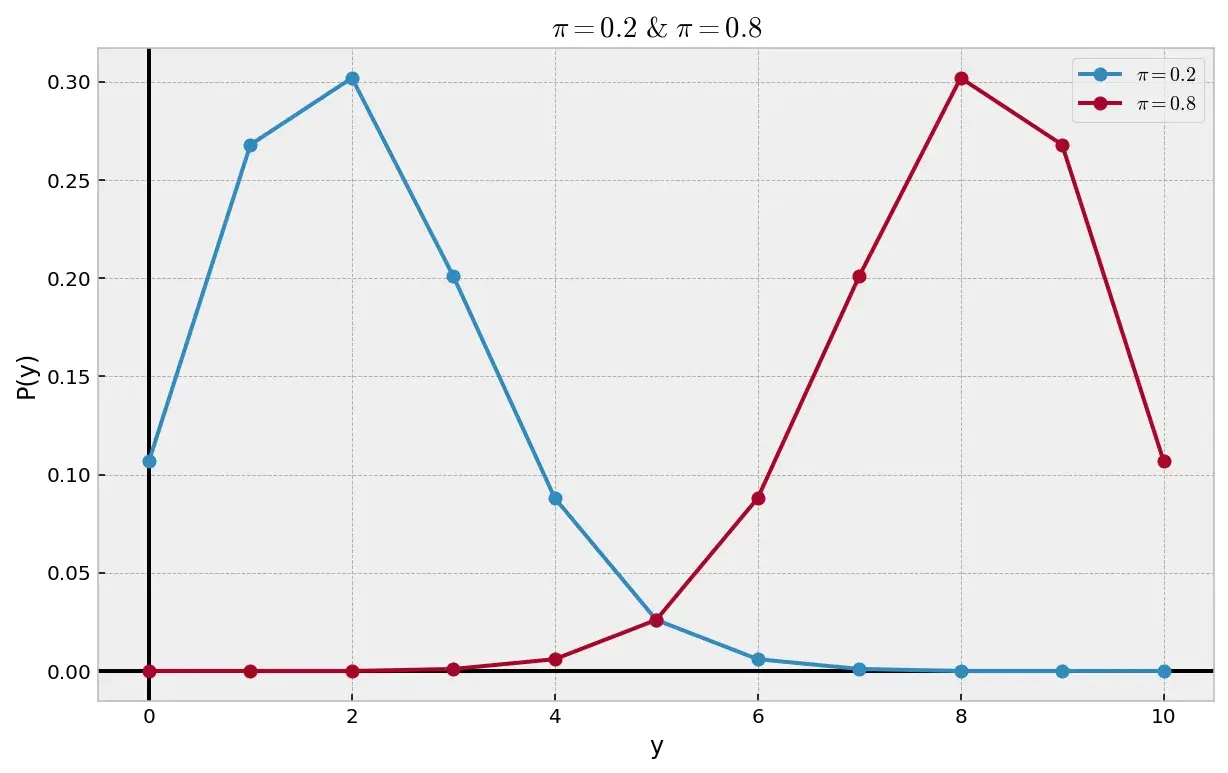
Для \(\pi = 0.8\) распределение будет предсказуемо выглядеть зеркальным отображением \(\pi = 0.2\):