Допустим, есть некоторая система, имеющая два состояния и есть монитор, который проверяет эту систему и возвращает 1 или 0, в зависимости от состояния. Примем \(p\) за соотношение значений всей генеральной совокупности. Так как генеральная совокупность принимает бинарные значения, то она имеет распределение Бернулли.
Также допустим, что получить весь массив данных, собранных об этой системе нет возможности, но для анализа предоставлена небольшая подвыборка, состоящая из 100 элементов. Можно посчитать \(\hat{p}\) —соотношение значений этой подвыборки. Допустим среднее количество состояний 1 для этой подвыборки равно 0.61.
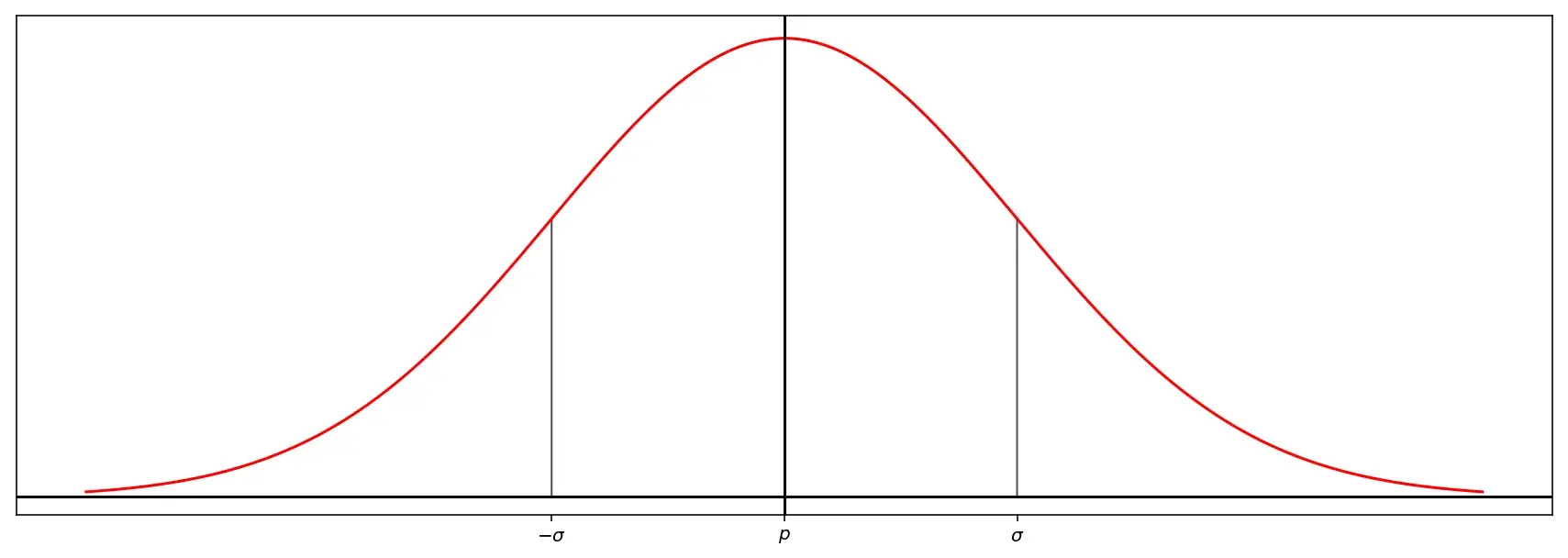
В соответствии с центральной предельной теоремой, распределение подвыборки будет приближено к нормальному, а его среднее выборочное будет приближено к среднему выборочному генеральной совокупности \(p\) со стандартным отклонением \(\sigma\):
Стандартное отклонение для подвыборки будет равно:
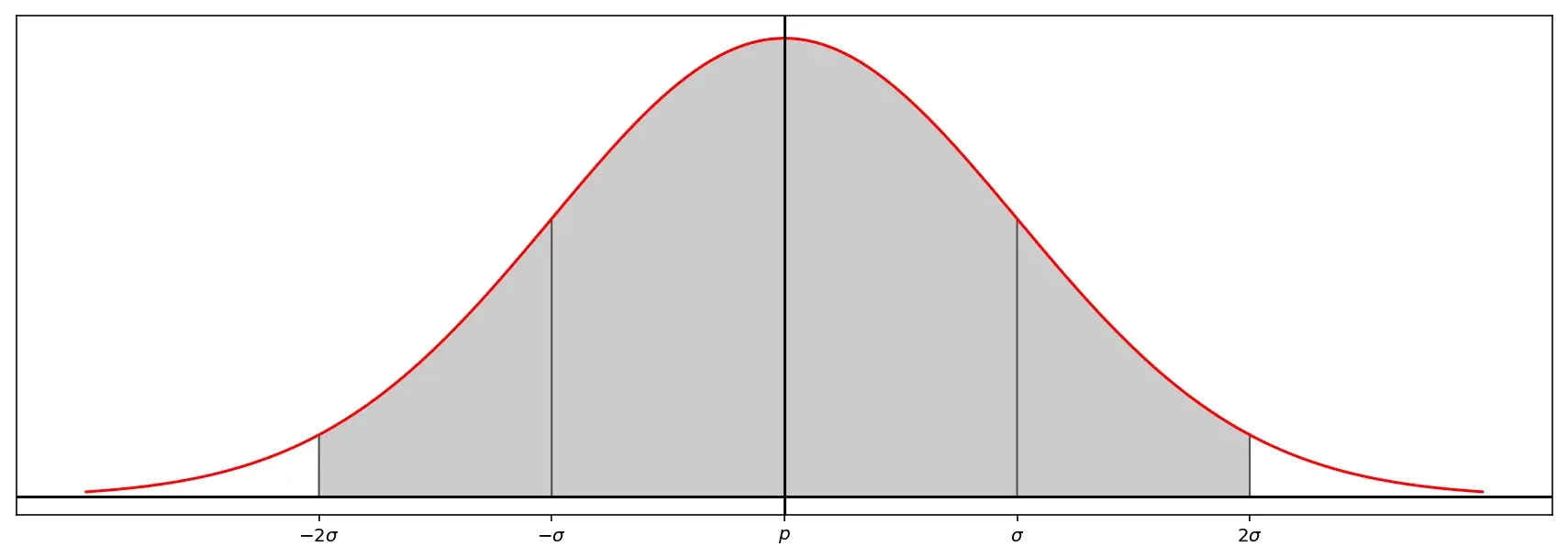
\[\sigma_{\hat{p}}=\sqrt{\frac{p(1-p)}{n}}\]Какова вероятность того, что \(\hat{p}\) лежит в пределах границ двух стандартных отклонений от \(p\)?
Так как в площадь под кривой в пределах двух стандартных отклонений попадает около 95 % значений, то вероятность того, что \(\hat{p}\) лежит в пределах границ двух стандартных отклонений от \(p\) будет также приблизительно равна 95 %.
Также существует 95 % вероятность того, что \(p\) находится в пределах двух стандартных отклонений \(\hat{p}\).
Однако, для того, чтобы посчитать точные значения стандартного отклонения подвыборки по формуле, указанной выше, необходимо знать значение \(p\). Вместо этого неизвестного значения, можно использовать приближенное значение \(\hat{p}\).
Для того, чтобы воспользоваться приближенным значением, нужно ввести новую статистику — стандартная ошибка SE:
\[\text{SE}_{\hat{p}}=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]Если подставить в формулу значение \(\hat{p} = 0.61\), то SE будет равно:
\[\text{SE}_{\hat{p}}=\sqrt{\frac{0.61(1-0.61)}{100}}\approx 0.049\]Получившееся значение 0.049 — это одно стандартное отклонение. Так как речь идет о 95%, то есть о двух стандартных отклонениях, то это значение следует умножить на два, а затем вычесть и прибавить к \(\hat{p}\).
\[ \begin{aligned} 0.61-2\cdot 0.049 &\approx 0.512\\ 0.61+2\cdot 0.049 &\approx 0.708 \end{aligned} \]Выходит, что с доверием, равным 95%, можно утверждать, что значение \(p\) лежит в границах от 0.512 до 0.708. Эти точки и есть границы доверительного интервала или, по-другому, доверительные пределы.
Нужно понимать, что доверительные пределы могут сдвигаться в ту или иную сторону в зависимости от значения \(\hat{p}\) подвыборки, однако, если раз за разом генерировать подвыборки и считать доверительные интервалы, эти интервалы будут в 95% случаев содержать \(p\).
Верный способ уменьшить разброс доверительных пределов — это увеличение размера подвыборки.