Для того, чтобы разобраться, как работают алгоритмы, ускоряющие градиентный спуск, нужно понять, что из себя представляют exponentially weighted averages. Если быть точным, в статистике это называется exponentially weighted moving averages.
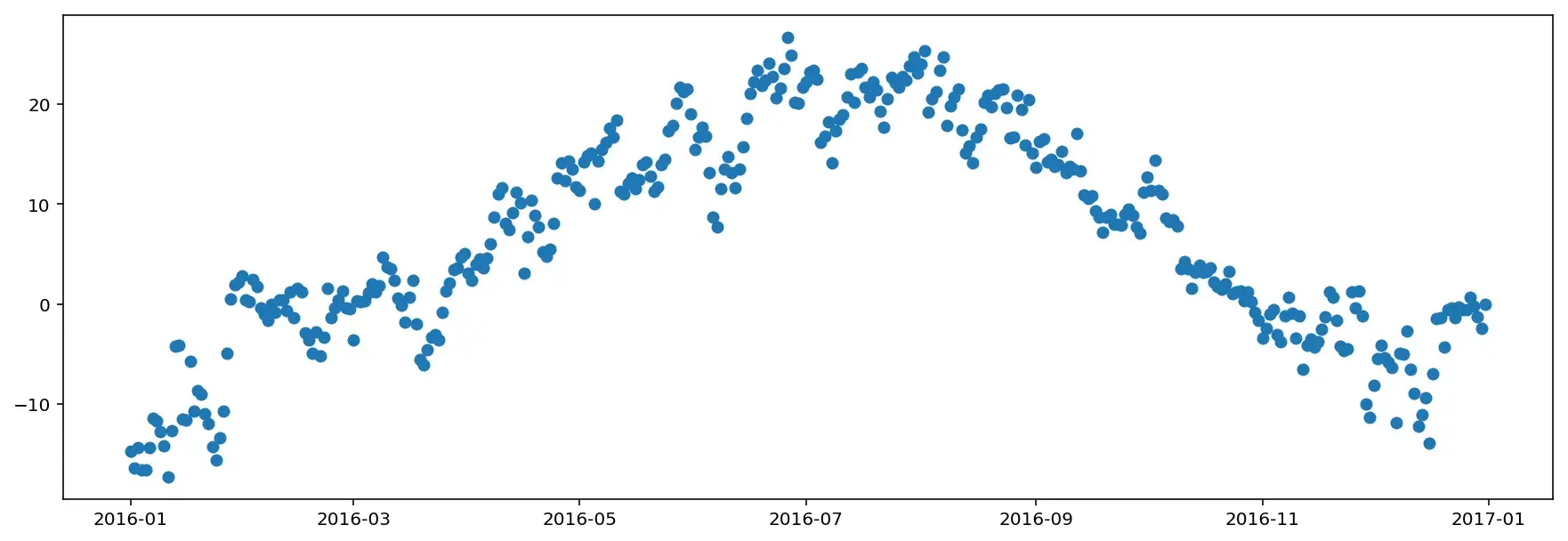
На графике ниже отображена средняя ежедневная температура в Москве в 2016 году, измеренная на метеостанции, которая располагается на ВДНХ.
Данные на графике выглядят довольно шумно и если необходимо построить тренд, на основании локального среднего или скользящего среднего, нужно поступить следующим образом. Необходимо инициализировать переменную \(V_0 = 0\) и для каждого следующего дня усреднить значение, пользуясь формулой:
\[ V_1 = 0.9V_0 + 0.1\Theta_1 \]Здесь \(\Theta_1\) — это температура в первый день, в нашем случае -14,7°C.
Для второго и последующих дней, нужно сделать точно так же, взяв предыдущее значение:
\[ \begin{aligned} V_2 &= 0.9V_1+0.1\Theta_2\\ V_3 &= 0.9V_2+0.1\Theta_3 \end{aligned} \]то есть, в общем случае формула выглядит так:
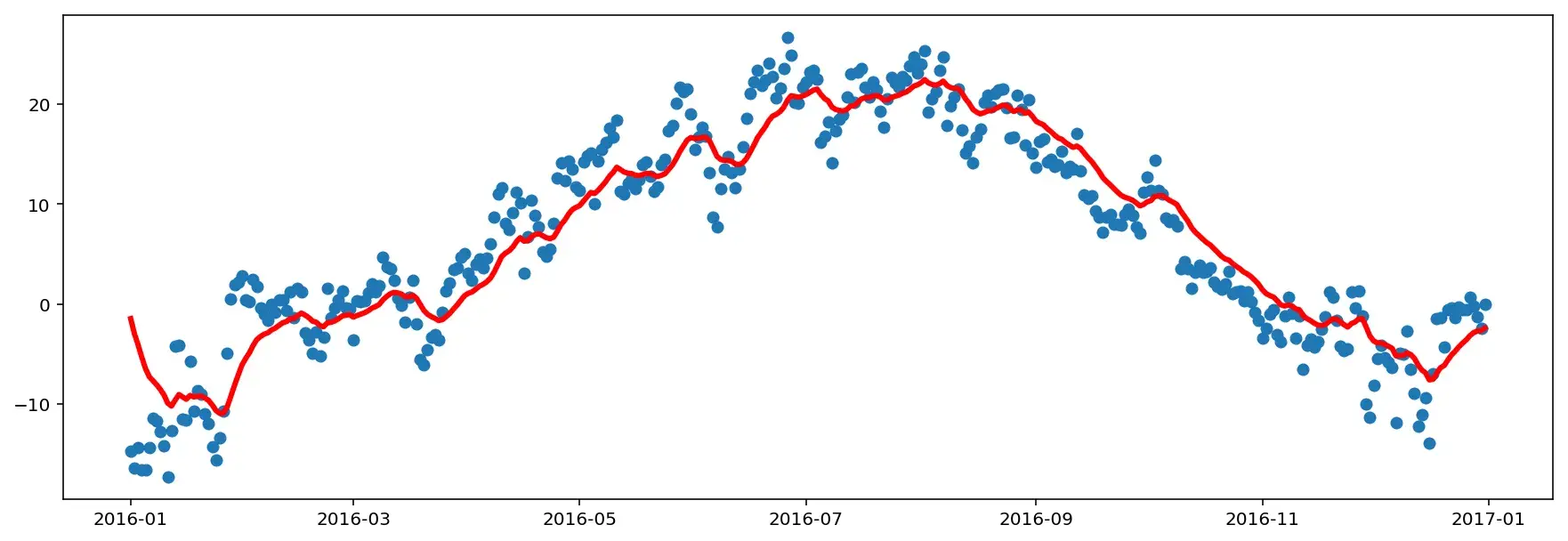
\[ V_t = 0.9V_{t-1}+0.1\Theta_t \]Если посчитать это для температуры в Москве в 2016 году и отобразить на графике, получится вот такая кривая, называемая exponential weighted average ежедневной температуры:
На самом деле множитель, стоящий перед \(V_{t-1}\) — это параметр \(\beta\), поэтому можно переписать формулу как:
\[ V_{t} = \beta V_{t-1}+(1-\beta)\Theta_t \]Значение \(V_t\) представляет собой усреднение температуры за несколько дней, количество которых можно посчитать как:
\[ V_t\approx \frac{1}{1-\beta} \]То есть, когда \(\beta = 0.9\) количество дней, по значениям температуры которых происходит усреднение, приблизительно равно \(10\). Теперь поглядим, что случится, если значение \(\beta\) станет близко к единице, например, пусть это будет \(0.98\). В этом случае, количество дней, по которым происходит усреднение увеличится до \(50\). На графике новая кривая отображена светло-зеленым цветом:
В этом случае кривая становится более гладкой и смещается вправо из-за того, что усреднение происходит в довольно большом окне, а когда окно большое, формула медленно адаптируется под изменения температуры. Когда значение \(\beta\) велико, то предыдущему значению дается большой коэффициент, а текущему — маленький. В случае, когда \(\beta = 0.98\), температура текущего дня получит коэффициент \(0.02\).
Если \(\beta\) принять за \(0.5\), то усреднение температуры будет происходить всего-лишь за два дня. На графике это будет выглядеть так:
Из-за того, что усреднение происходит всего-лишь за два последних дня, кривая получается довольно шумной и неустойчивой к выбросам.