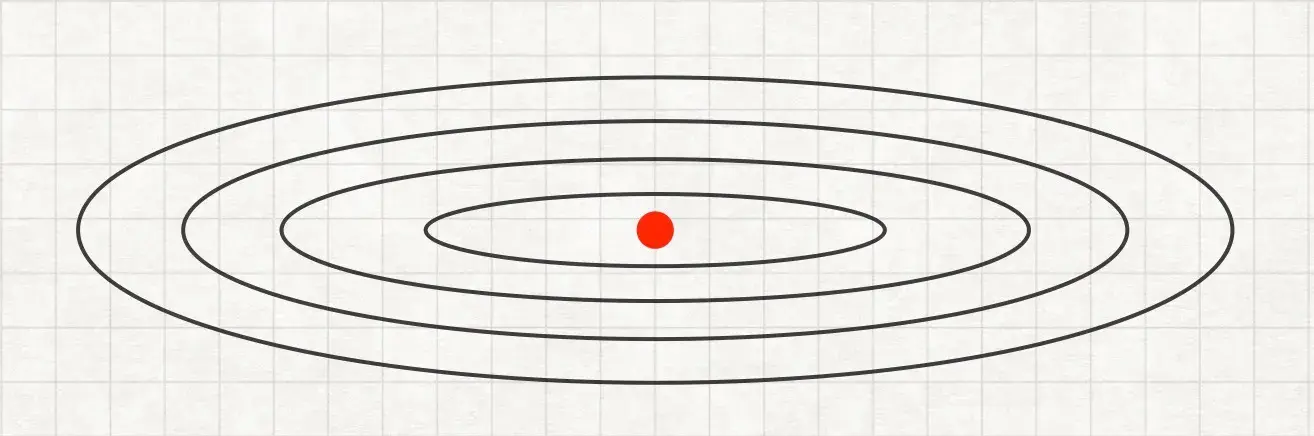
Представим, что нужно оптимизировать cost function, которая выглядит как-то так:
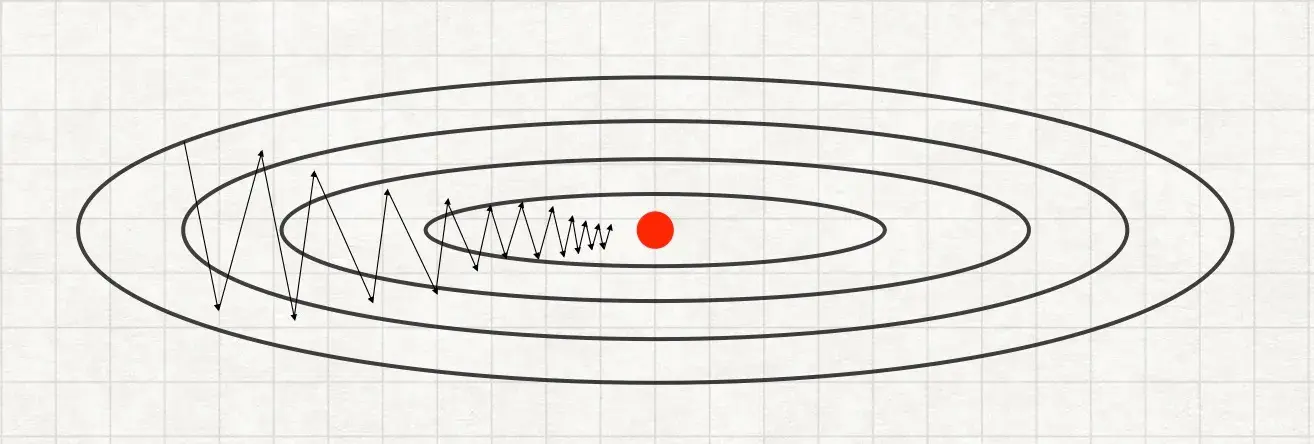
Запускаем градиентный спуск и видим какую-то такую картину:
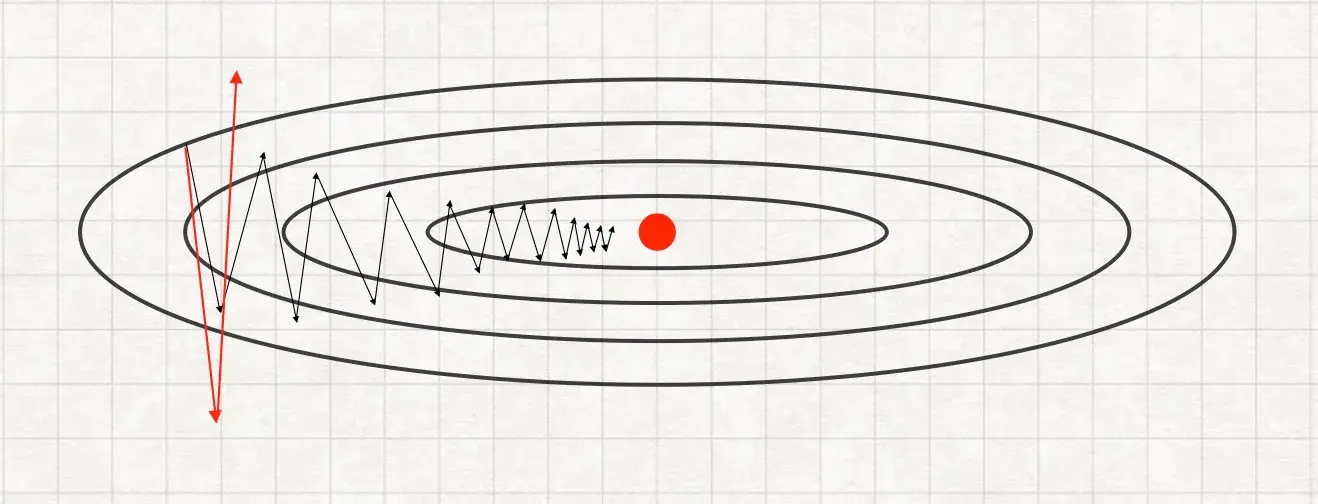
Видно, что градиентный спуск выполняет слишком много шагов, при этом в вертикальном направлении шаг получается слишком размашистым. Этот размашистый шаг замедляет спуск и не позволяет увеличить величину шага \(\alpha\), потому что если увеличить значение \(\alpha\), то картина станет такой:
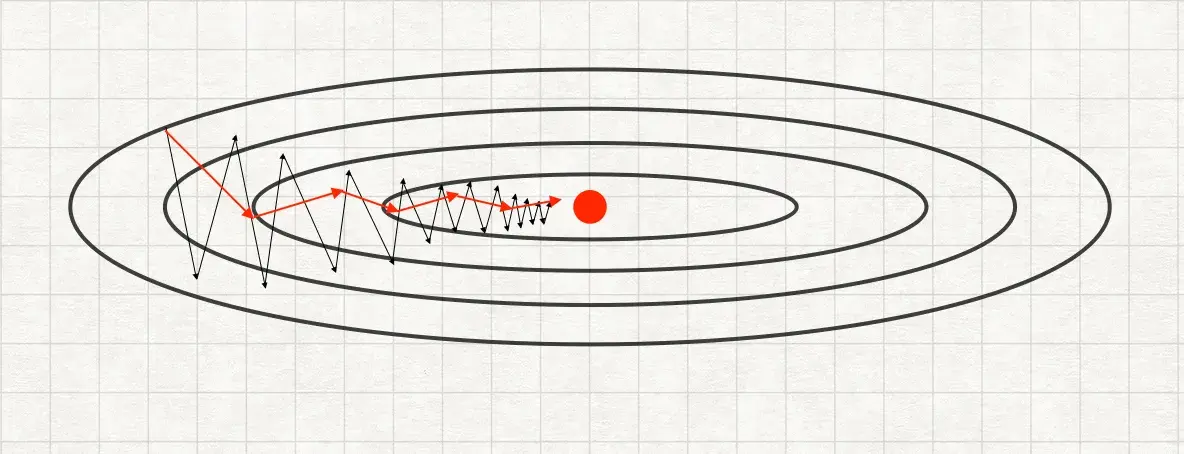
Получается, что для оптимальной работы спуска в вертикальном направление скорость должна быть ниже, чем в горизонтальном. Для этого можно воспользоваться формулой exponential wighted averages и на кажом шаге \(t\) считать производные для параметров как:
\[ \begin{aligned} V_{dw} &= \beta V_{dw} + (1-\beta)\frac{\partial\mathcal{L}}{\partial w} \\ V_{db} &= \beta V_{db} + (1-\beta)\frac{\partial\mathcal{L}}{\partial b} \end{aligned} \]и обновлять параметры не при помощи значения производной, а при помощи вычисленных \(V_{dw}\) и \(V_{db}\):
\[ \begin{aligned} w &:= w - \alpha V_{dw}\\ b &:= b - \alpha V_{db} \end{aligned} \]При таком обновлении параметров шаги градиентного спуска в вертикальном направлении уменьшатся, в горизонтальном — увеличатся, что приведет к более быстрому схождению.