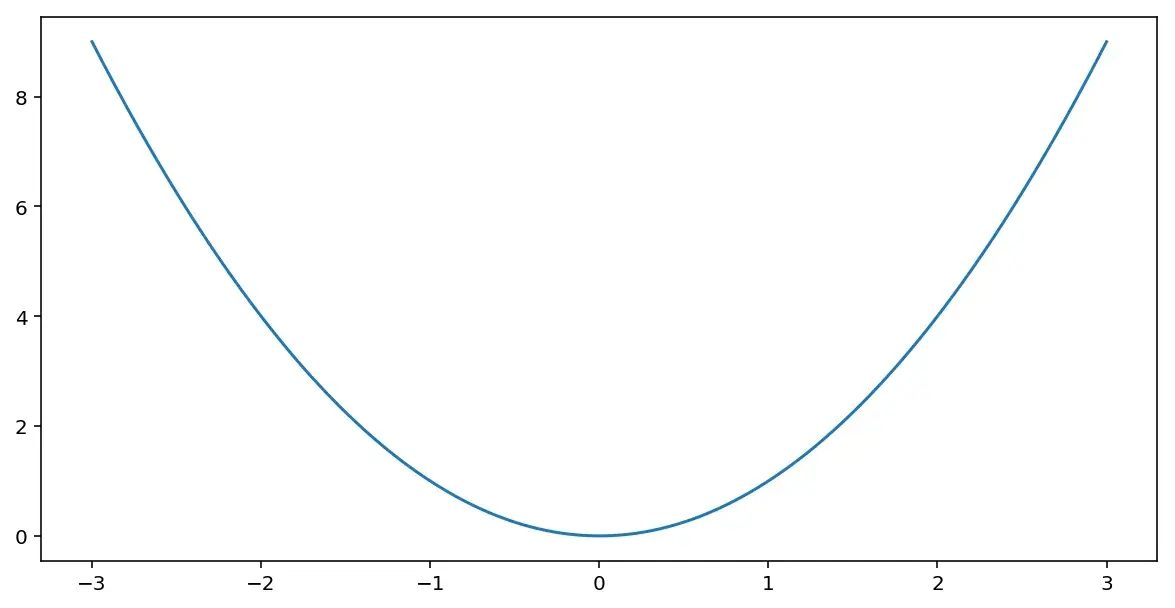
Для понимания в общих чертах, как работает градиентный спуск, представим, что у нас есть функция с одним параметром \(\mathcal{J}(w)\), которую нужно минимизировать. Например, она может выглядеть вот так:
Для этого нужно произвести серию шагов, на каждом из которых берется текущее значение параметра \(w\) из него вычитается произведение параметра \(\alpha\) на производную:
\[w:=w-\alpha\frac{d\mathcal{J}(w)}{dw}\]и это повторяется до тех пор, пока алгоритм не сойдется.
Параметр \(\alpha\) — это learning rate, задающий размер шага градиентного спуска.
Картинка выше иллюстрирует работу алгоритма. Спуск начинается в некоей точке. Дальше производится серия шагов с вычислением производной и обновлением значения переменной до тех пор, пока не будет достигнут глобальный минимум.
Пример выше приведен для функции с одним параметром, однако для логистической регрессии используется два параметра, поэтому для нее на каждом шаге спуска будет производиться обновление двух параметров:
\[ \begin{aligned} w &:= w-\alpha\frac{\partial\mathcal{J}(w,b)}{\partial w}\\ \\ b &:= b-\alpha\frac{\partial\mathcal{J}(w,b)}{\partial b} \end{aligned} \]