На результат работы алгоритма оказывает влияние изначальная инициализация переменной оценочного вознаграждения \(Q\). В статистике это влияние называется bias.
Для методов с переменным значением константы \(1/n\), как в этой статье, влияние bias исчезает в тот момент, когда каждое действие оказалось выбрано хотя бы один раз. В том же случае, когда коэффициент \(\alpha\) — константа, bias присутствует постоянно, хотя его влияние и снижается с течением времени.
Оказывается, правильная инициализация \(Q\) может сподвигнуть даже жадный алгоритм заняться исследованием. Так, если переменную \(Q\) инициализировать не нулями, как это делалось в предыдущей статье, а, например, прибавить к каждому значению 5, то при любом действии на начальном этапе награда оказывается значительно ниже изначального оценочного ожидания. В результате все варианты действий будут опробованы несколько раз прежде, чем начнётся схождение. То есть, даже в случае использования жадного алгоритма будет производиться исследование.
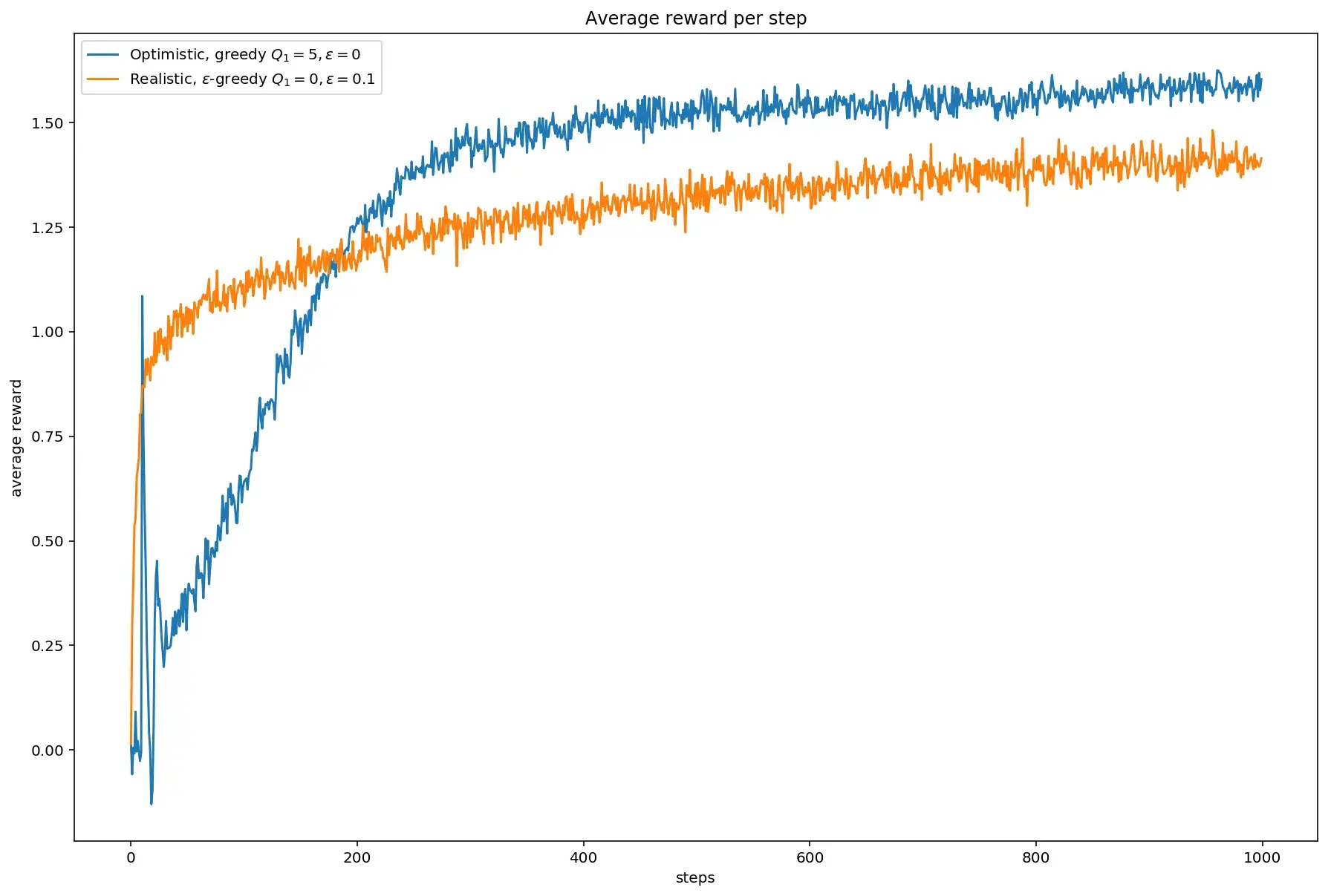
Для примера, сравним два варианта. В первом оптимистичном переменная \(Q\) при инициализации увеличена на 5, а параметр 𝜺 равен нулю, то есть применён жадный алгоритм. Во втором — \(Q\) инициализирован нулями, а параметр \(\varepsilon\) равен 0.1. В обоих случаях \(\alpha = 0.1\):
Хотя жадный оптимистичный алгоритм начинает сходиться немного медленнее, в итоге оказывается, что среднее вознаграждение у него выше.
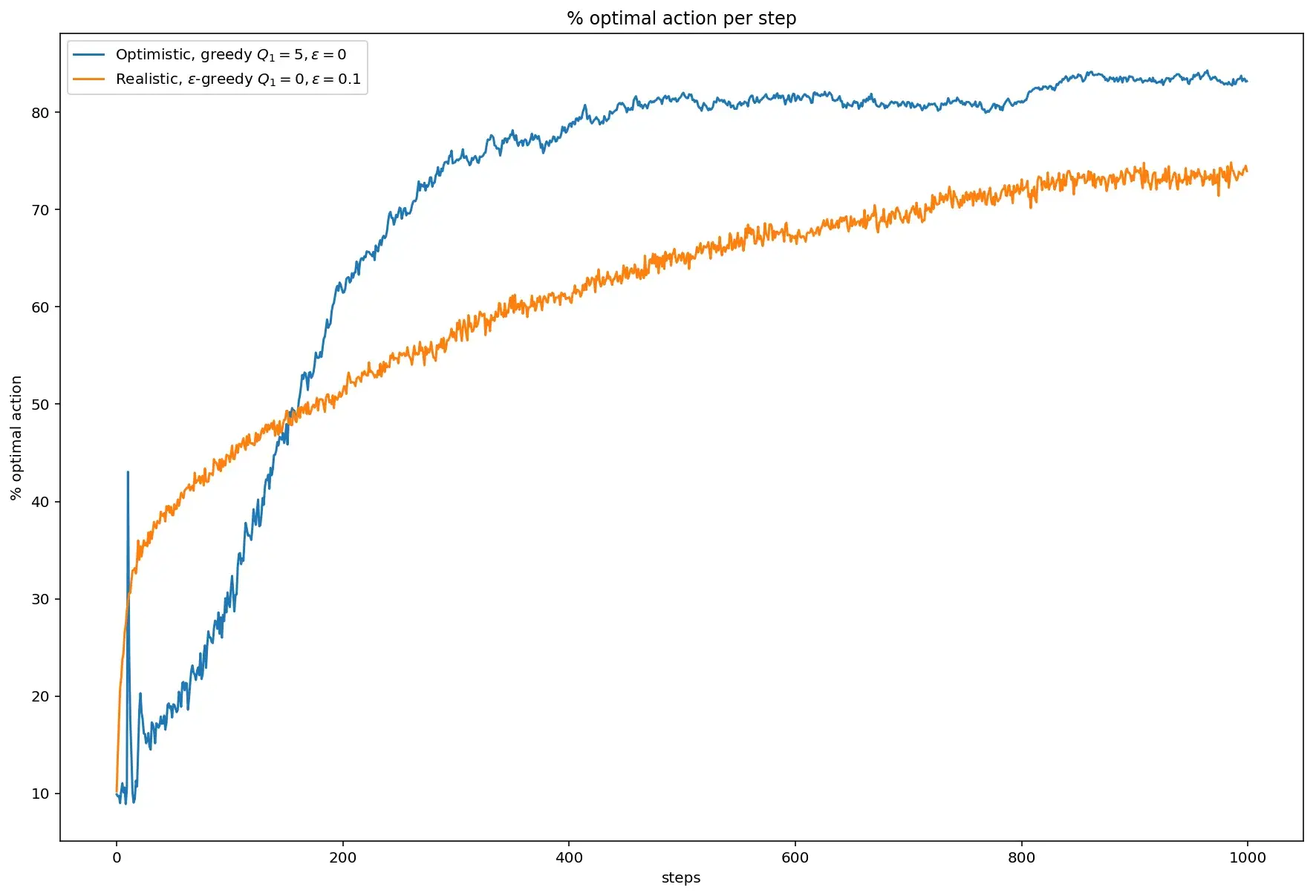
Тоже самое можно сказать и о проценте оптимальных действий: