Вероятность количества успешных событий в биномиальной выборке вычисляется по формуле:
\[P(y) = \frac{n!}{y!(n-y)!}\pi^y (1-\pi)^{\pi-y}\]Если вернуться к предыдущей статье, то можно сказать, что зная, что на каждом этаже расположено пять квартир и только в одной из них живет знакомый (то есть вероятность встретить знакомого на кажом этаже это параметр \(\pi\) равный 0.2), можно вычислить, например, вероятность того, что пройдя по десяти этажам (\(n = 10\)) и звоня в одну случайную квартиру, я не встречу ни одного знакомого. Всё просто, нужно подставить эти значения в формулу и посчитать.
Однако, может быть другая ситуация. Допустим, есть подъезд в котором живут знакомые на десяти этажах, но сколько на каждом этаже квартир, и в скольких квартирах живут эти знакомые, — неизвестно. Для простоты будем считать, что это соотношение одинаково на каждом этаже. Другими словами, мне известны параметры \(n = 10\) и \(y = 0\), но параметр \(\pi\) не определен. В этом случае, подставив известные значения в формулу, получаем функцию, в которой \(\pi\) может принимать значения в промежутке от нуля до единицы (помните, что это вероятность успеха встретить знакомого на каждом этаже):
\[P(0)=\frac{10!}{0!\cdot 10!}\pi^0(1-\pi)^{10}=(1-\pi)^{10}\]Такая функция называется функцией правдоподобия (англ. likelihood function). Формально, для этого конкретного случая, её формулу можно записать вот так:
\[l(\pi)=(1-\pi)^{10}, \ 0\le \pi \le 1\]Теперь попробуем подставить вместо \(\pi\) какие-нибудь значения и поглядеть, что получится на выходе. Для начала пусть это будет 0.4:
\[l(0.4) = (1-0.4)^{10}= 0.006\]То есть, если для каждого события вероятность успеха \(\pi\) равна 0.4, то вероятность того, что не будет встречено ни одного знакомого на всех десяти этажах будет равна 0.006.
При \(\pi = 0.2\), соответственно, получается 0.107:
\[l(0.2) = (1-0.2)^{10}= 0.107\]А если принять \(\pi = 0\), вероятность окажется равной единице:
\[l(1) = (1-0)^{10}= 1\]Выходит, что при \(\pi = 0\), функция принимает максимально возможное значение. Это и есть оценка максимального правдоподобия (англ. maximum likelihood estimate).
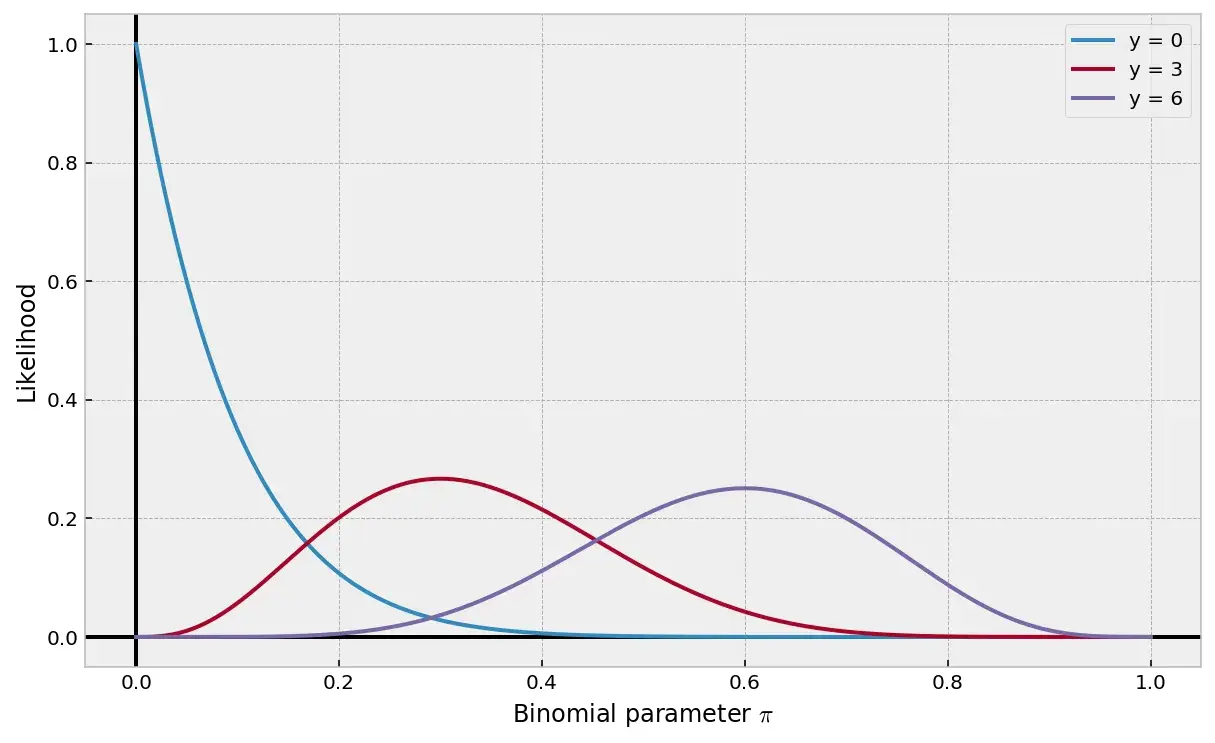
Для наглядности графики функций правдоподобия для трёх различных \(y\):
На изображении видно, что максимальное правдоподобие для \(p = 0\) достигается при параметре \(\pi = 0\), для \(p = 3\) при \(\pi = 0.3\), для \(p = 6\) при \(\pi = 0.6\).
То есть, максимальным правдоподобием для биномиального параметра \(\pi\) оказывается среднее значение успешных исходов подвыборки. Другими словами, если мы ожидаем, что должно быть 6 успешных исходов из 10, то, приняв успешные исходы за единицу, а неудачные — за ноль, можем получить оценку максимального правдоподобия \(\pi\) таким простым способом:
\[\hat{\pi} = \frac{0+0+0+0+1+1+1+1+1+1}{10}=0.6\]https://ru.wikipedia.org/wiki/Метод_максимального_правдоподобия
https://ru.wikipedia.org/wiki/Функция_правдоподобия
A. Agresti “An introduction to categorical data analysis”