PReLU или Parametric ReLU — это логическое развитие обыкновенной активационной функции ReLU. Основное отличие между ними состоит в том, что у PReLU есть обучаемые параметры.
PReLU определяется следующей формулой:
\[f(y_i)= \begin{cases} y_i, &y_i > 0\\ a_iy_i, &y_i \le 0 \end{cases}\]В этой формуле \(y_i\) — это то, что приходит на вход активационной функции канала \(i\), а \(a_i\) — это коэффициент, отвечающий за наклон отрицательной части. Индекс \(i\) у параметра \(a_i\) показывает, что нелинейная активация может быть разной для разных каналов. При этом, если \(a_i\) приравнять к нулю, активационная функция превратится в простую ReLU.
Формулу выше можно записать ещё и немного по-другому:
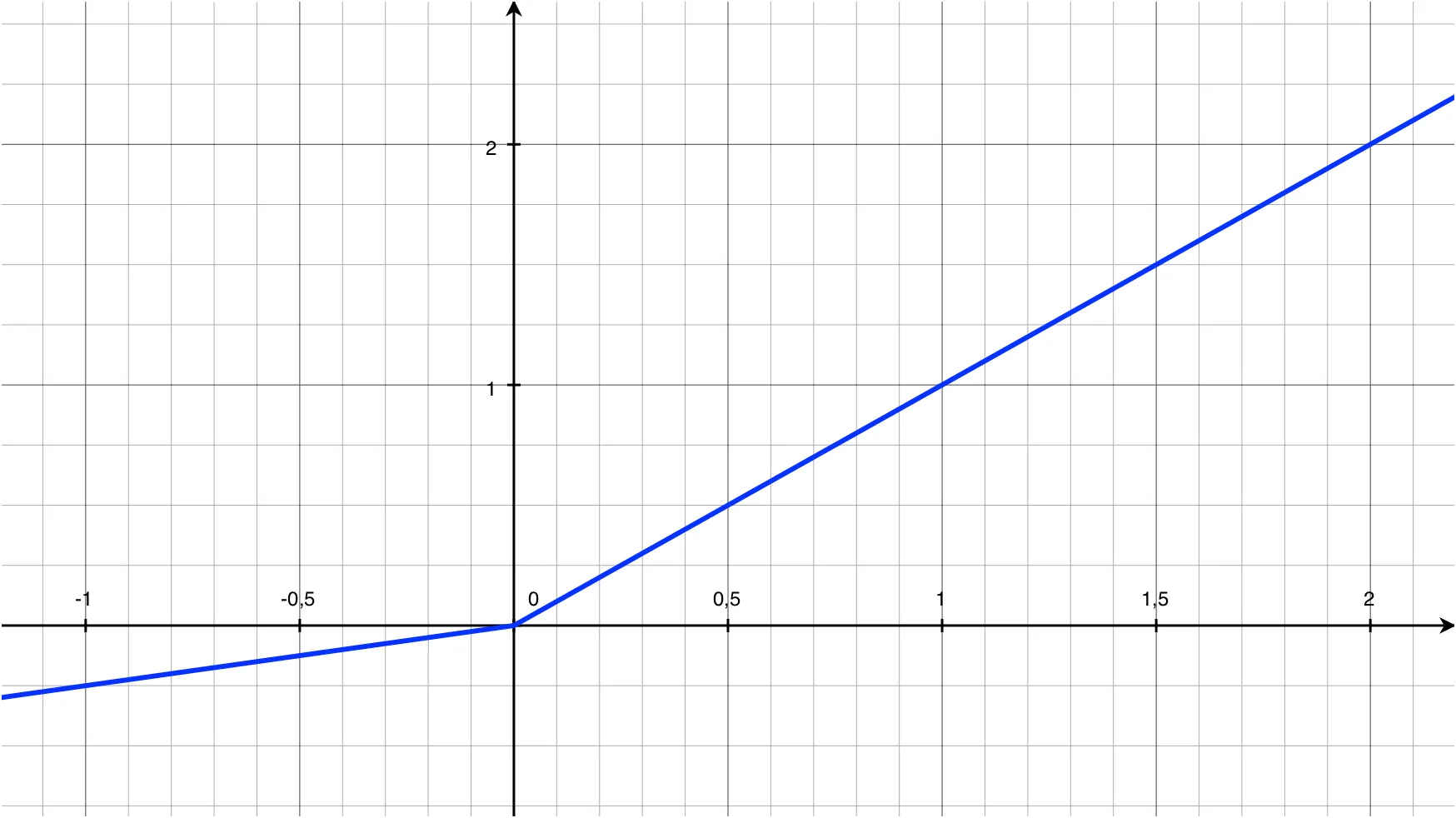
\[f(y_i) = \max(0, y_i) + a_i\min(0, y_i)\]Вот как выглядит PReLU на графике, при параметре \(a_i = 0.25\):
Если значение параметра \(a_i\) мало и фиксированно, например 0.01, PReLU становится Leaky ReLU (LReLU). Основной идеей создания LReLU было устранение нулевого градиента, однако, по факту, LReLU даёт ничтожно малый прирост точности, по сравнению с обычной ReLU, поэтому о ней нет смысла говорить.
Функция PReLU хороша тем, что с её добавлением, количество параметров сети увеличивается незначительно: общее количество новых параметров каждого слоя всего лишь равно количеству каналов этого слоя.
PReLU может быть channel-shared. Это означает, что значение параметра \(a\) будет общим для всех каналов. В этом случае в формуле у параметра не будет индекса:
\[f(y_i) = \max(0, y_i) + a\min(0, y_i)\]Оптимизация
Градиент параметра \(a_i\) для одного слоя вычисляется по формуле:
\[\frac{\partial \mathcal{E}}{\partial a_i} = \sum_{y_i}\frac{\partial \mathcal{E}}{\partial f(y_i)} \frac{\partial f(y_i)}{\partial a_i}\]где \(\mathcal{E}\) — это оптимизируемая функция.
Левая часть произведения под знаком суммы — это градиент, пришедший с более глубокого слоя:
\[\frac{\partial \mathcal{E}}{\partial f(y_i)}\]а правая часть — градиент активации, который вычисляется как:
\[\frac{\partial f(y_i)}{\partial a_i} = \begin{cases} 0, &y_i > 0\\ y_i, &y_i \le 0 \end{cases}\]Для channel-shared варианта в формулу добавляется ещё один знак суммы:
\[\frac{\partial \mathcal{E}}{\partial a_i} = \sum_{i}\sum_{y_i}\frac{\partial \mathcal{E}}{\partial f(y_i)} \frac{\partial f(y_i)}{\partial a_i}\]потому как в этом случае требуется суммировать все каналы слоя.
Обновление значения параметра \(a_i\) производится по формуле:
\[\Delta a_i := \mu \Delta a_i + \varepsilon\frac{\partial \mathcal{E}}{\partial a_i}\]в которой \(\mu\) — это momentum, а \(\varepsilon\) — скорость обучения.
При обновлении значения параметра \(\varepsilon\) не используется L2-регуляризация (weight decay), поскольку она быстро приводит значение параметра к нулю, а это превращает PReLU в обычную ReLU.
Kaiming He et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv:1502.01852 [cs.CV]