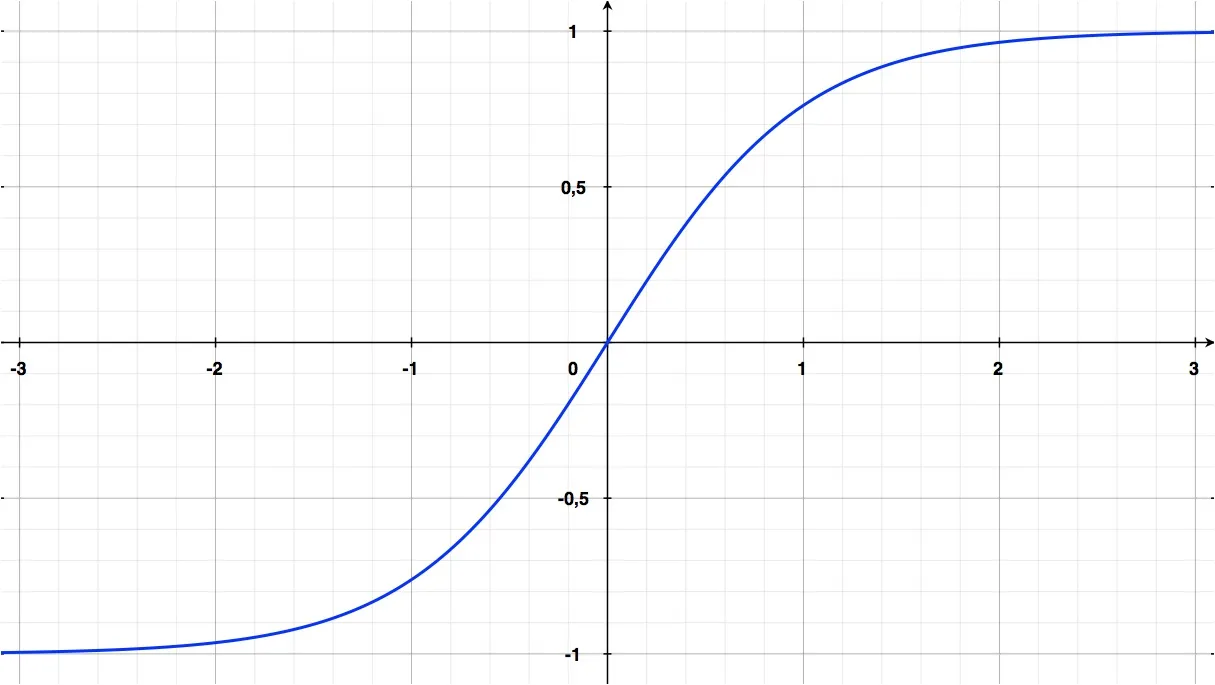
В прошлом десятилетии стандартной активационной функцией для сетей считалась \(\tanh(x)\) или, по-другому, hyperbolic tangent function:
\[f(x)=\tanh(x)\]График этой функции очень похож на сигмоиду, однако, в отличие от последней, границы оси y которой лежат в пределах [0; 1], границы \(\tanh(x)\) лежат в пределах [-1; 1]:
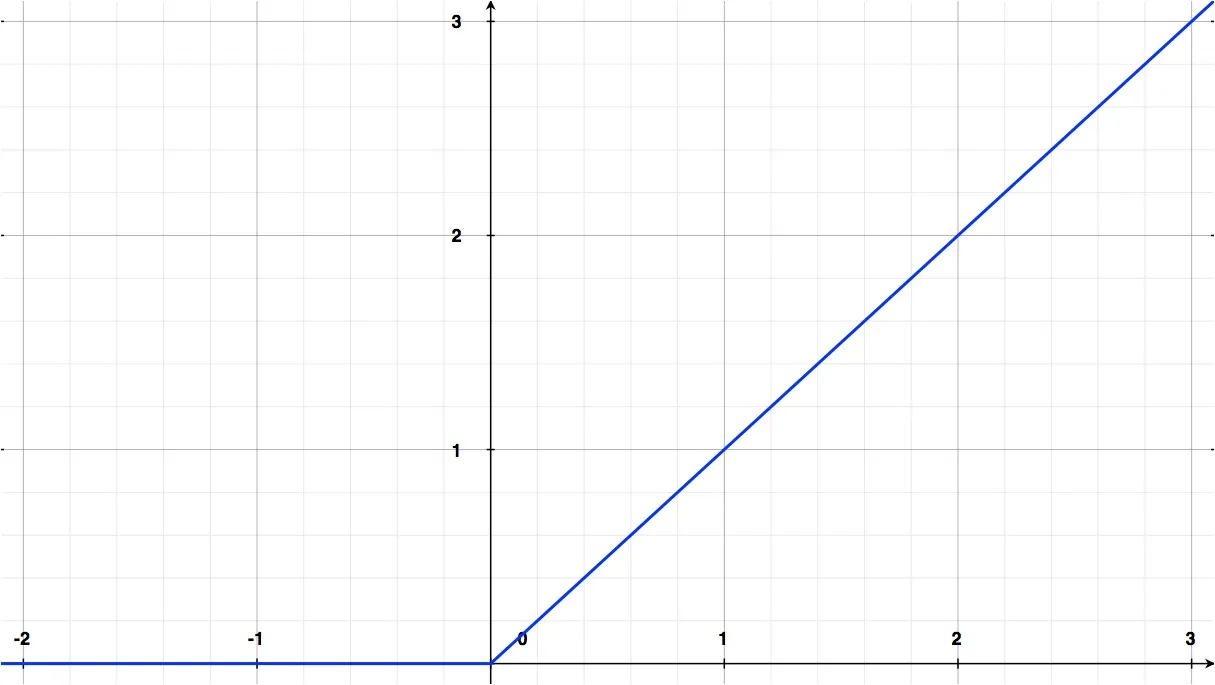
В современном мире чаще всего взамен \(\tanh\) используют ReLU (Rectified Linear Units), которая представляет собой функцию, которая возвращает положительное или нулевое значение аргумента:
\[f(x)= \max(0,x)\]Выглядит ReLU на графике вот так:
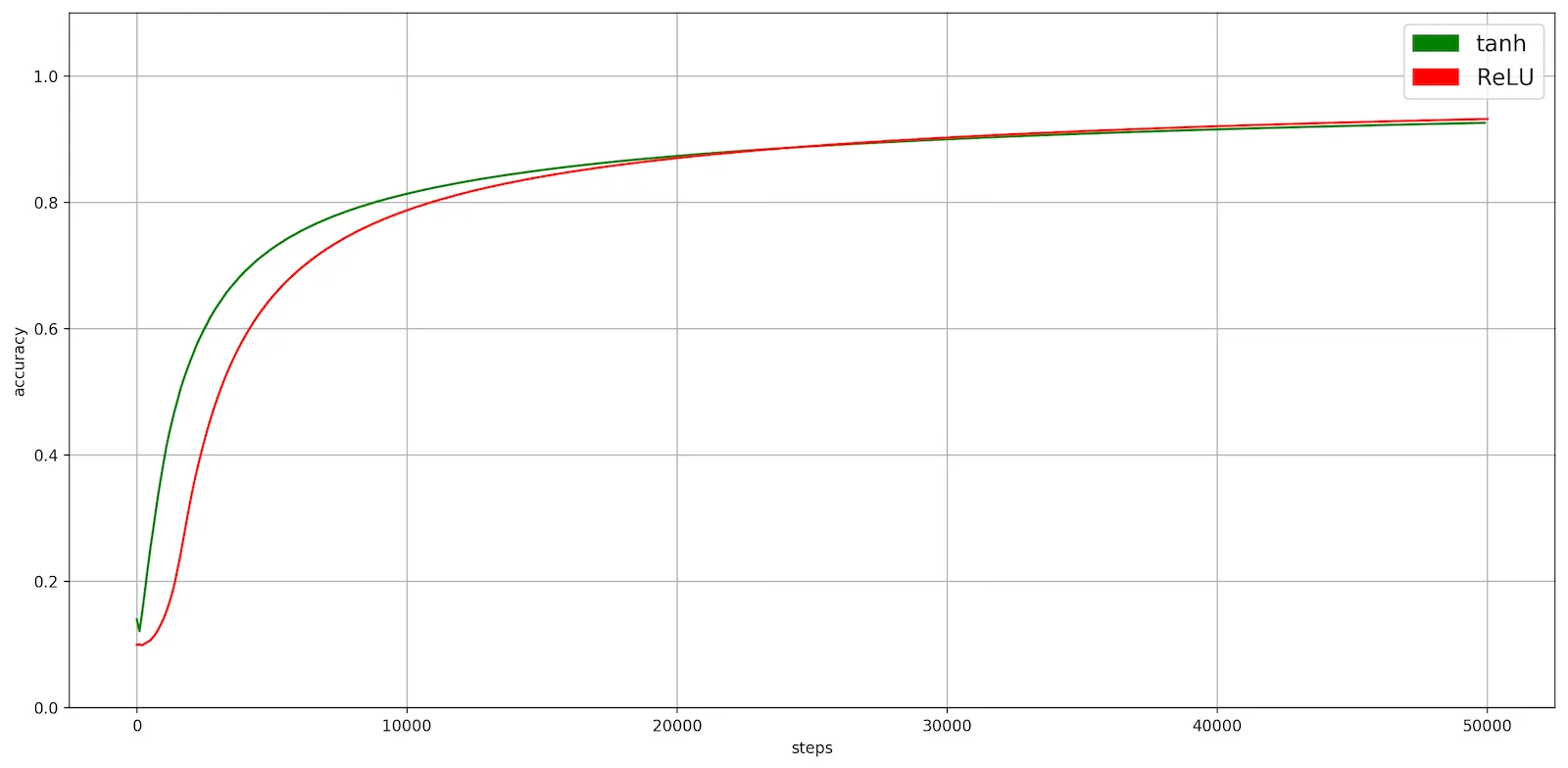
Замена в сети LeNet-5 активационной функции tanh на ReLU (без изменения других параметров) дала 0,5% прирост accuracy на тренировочных и тестовых данных:
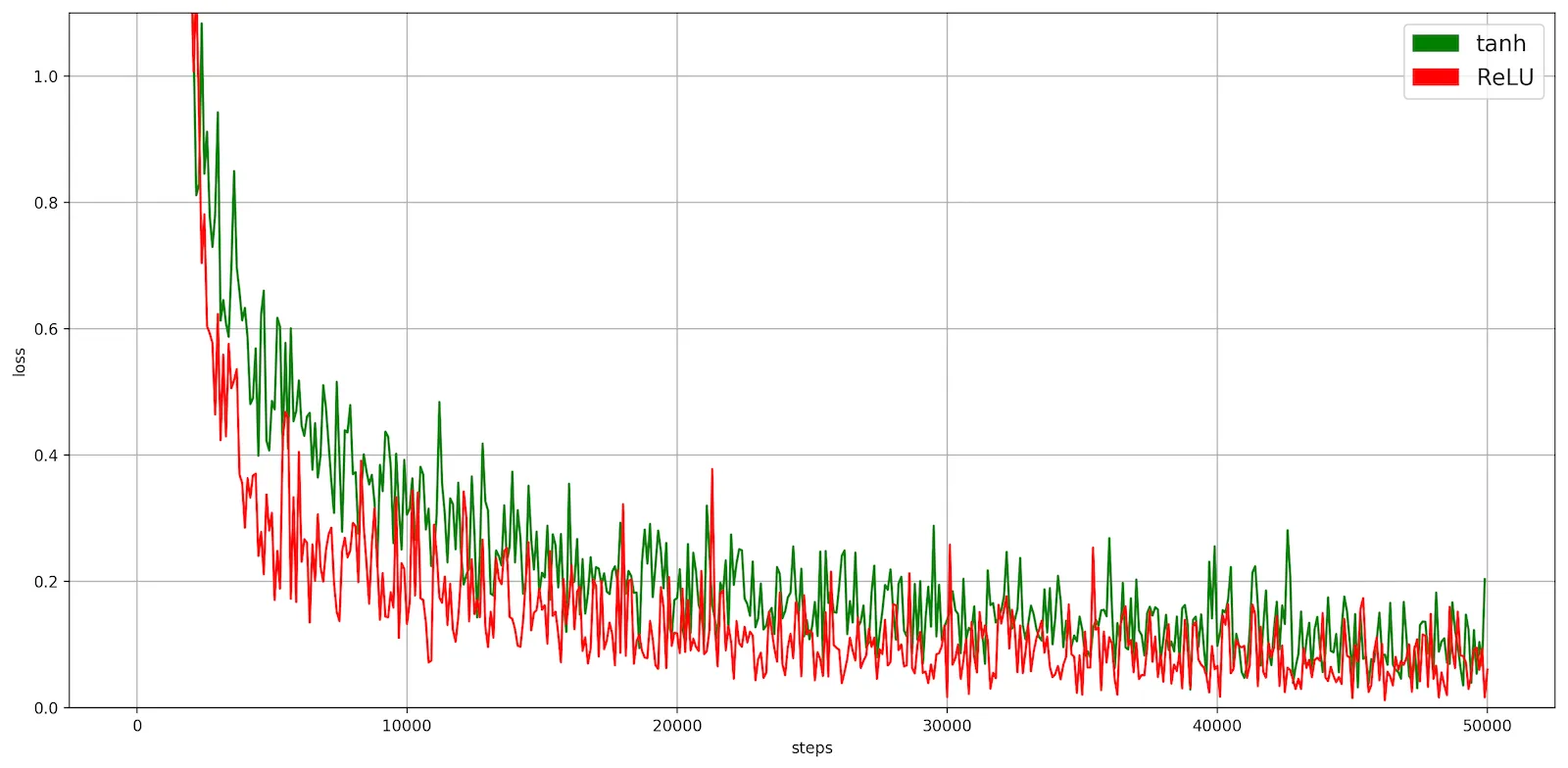
Значение loss уменьшается заметно быстрее у ReLU. На тестовых данных loss падает с 0.09352 до 0.06445:
Может показаться, что из-за такого маленького прироста вообще нет смысла говорить о замене активационной функции, однако, LeNet-5 слишком простая и неглубокая сеть, к тому же её обучение проводилось на довольно маленьких изображениях.
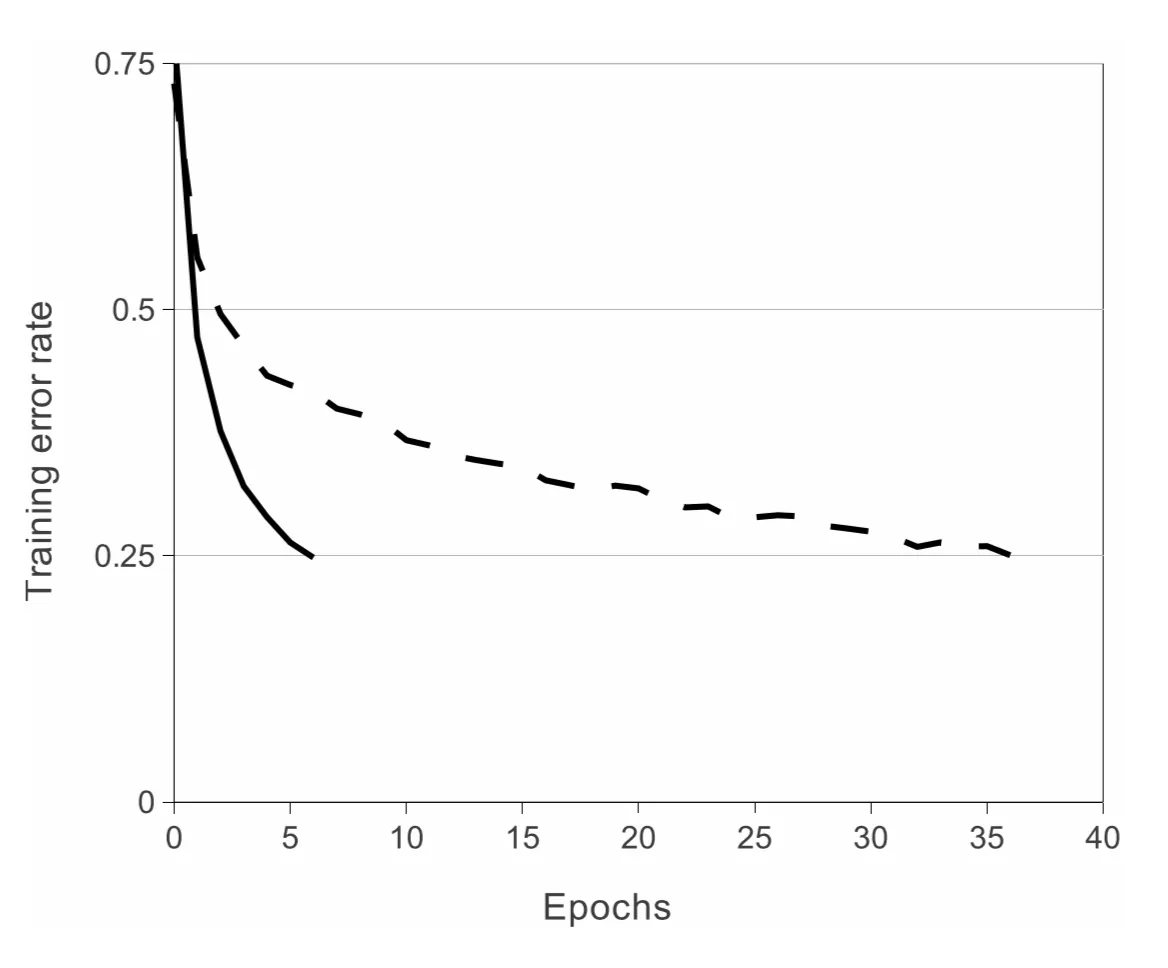
В статье, описывающей сеть AlexNet (Krizhevsky et al., 2012), сказано, что у исследователей на датасете CIFAR-10 значение training error rate падало с функцией ReLU в шесть раз быстрее, чем \(\tanh\):