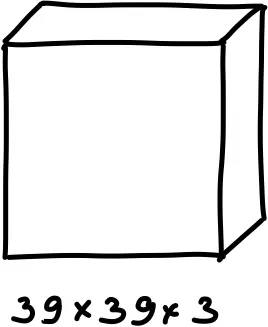
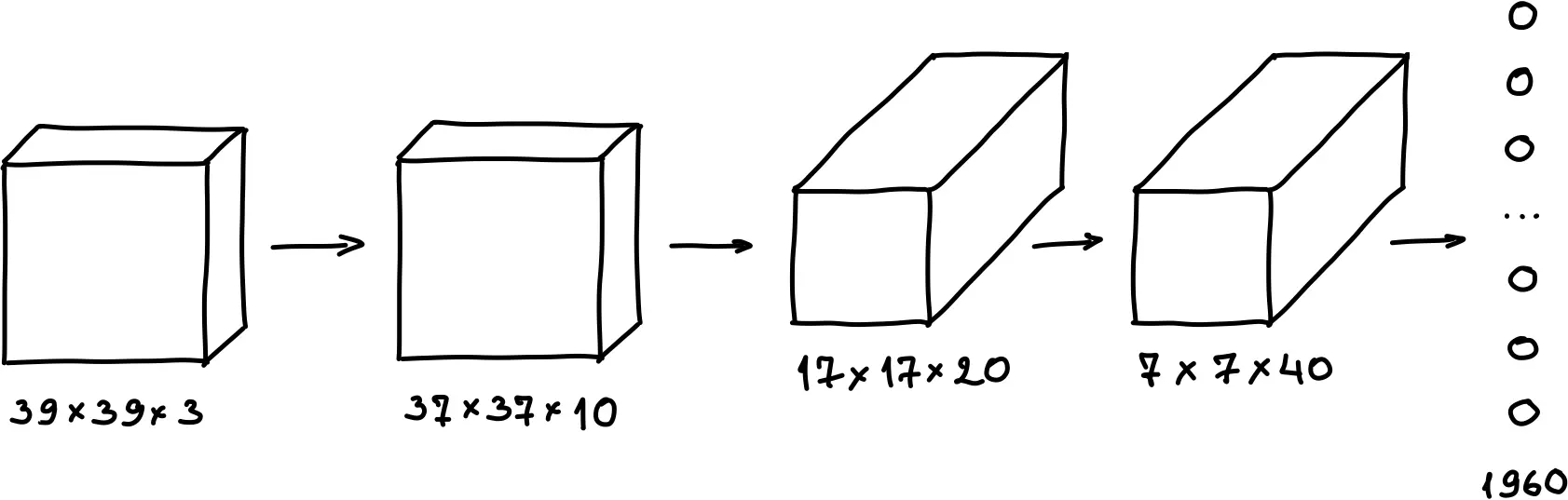
Есть изображение размером 39 х 39 х 3:
Так как у него высота и ширина равны, то:
\[n_H^{[0]} = n_W^{[0]} = 39\]Изображение цветное, то есть у него три слоя:
\[n_c^{[0]}=3\]первый слой
Padding будет valid:
\[p^{[1]}=0\]Stride по умолчанию равен единице:
\[s^{[1]} =1\]Количество слоёв фильтра равно количеству слоёв исходного изображения:
\[f^{[1]} = 3\]Воспользуемся формулой, чтобы посчитать размерность матрицы, после первого слоя CNN:
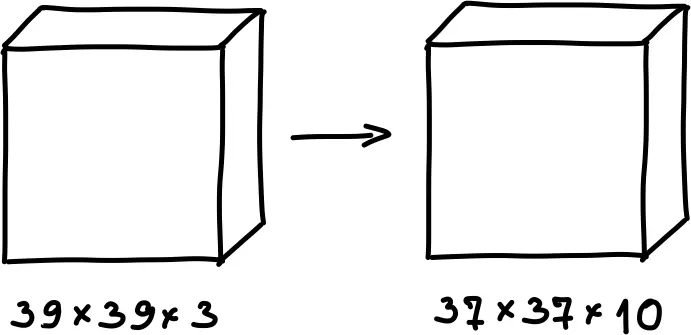
\[\frac{n+2p-f}{s}+1 = \frac{39+0-3}{1}+1 = 37\]Фильтров в первом слое будет 10, поэтому на выходе получится:
Параметры \(n_H\) и \(n_W\) получившегося тензора будут равны:
\[n_H^{[1]} = n_W^{[1]} = 37\]Количество слоев равно 10:
\[n_c^{[1]} = 10\]второй слой
Пропустим получившиеся данные через ещё один свёрточный слой, с пятислойными фильтрами:
\[f^{[2]} = 5\]Valid padding:
\[p^{[2]} = 0\]stride равный двум:
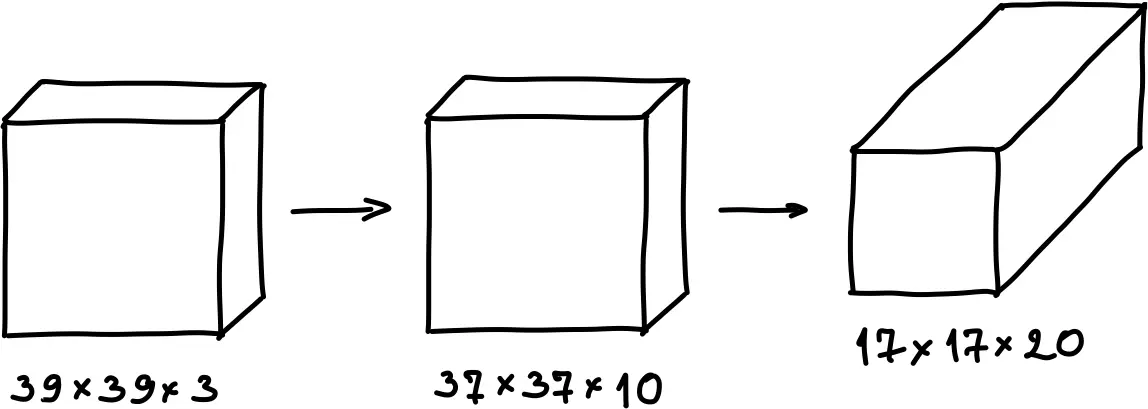
\[s^{[2]}=2\]и 20 фильтров. На выходе получится объём 17 х 17 х 20:
\(n_H\) и \(n_W\):
\[n_H^{[2]} = n_W^{[2]}=17\]количество слоёв:
\[n_c=20\]третий слой
Теперь пропустим через ещё один свёрточный слой с пятислойными фильтрами:
\[f^{[3]} = 5\]и stride равный двум:
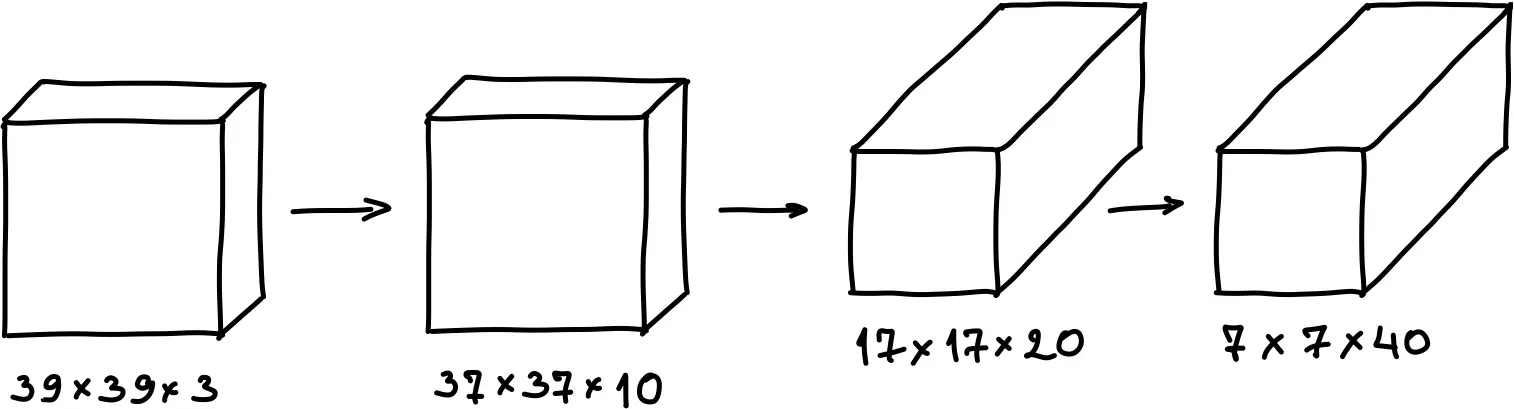
\[s^{[3]}=2\]и 40 фильтров. На выходе получится объём 7 х 7 х 40:
финальный слой
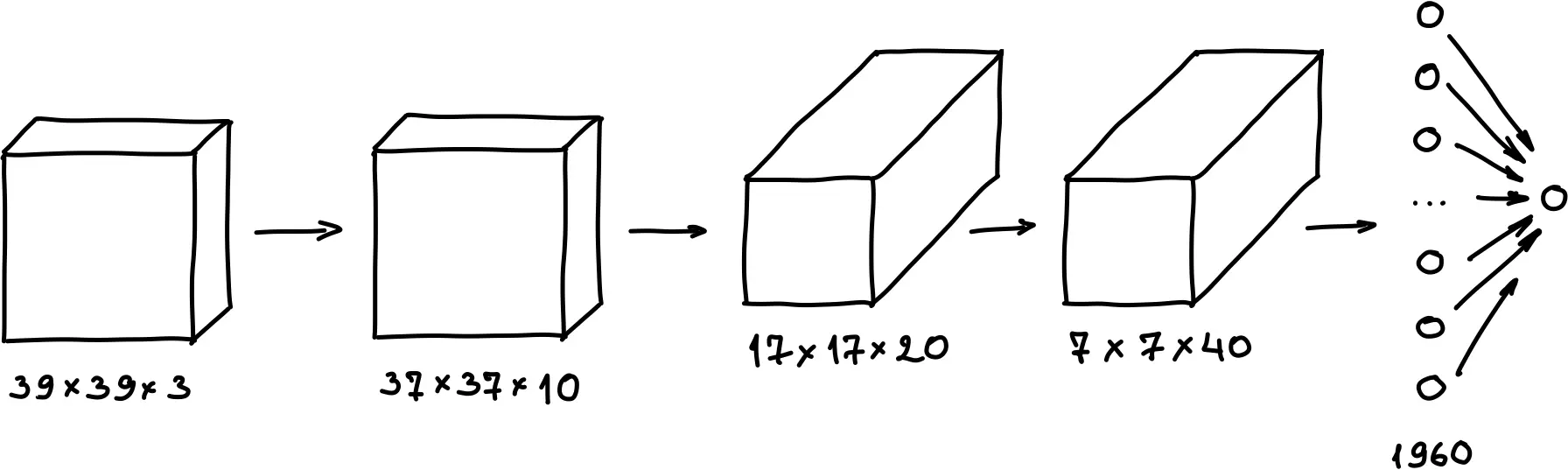
Затем получившийся объем выстраивается в один длинный вектор:
получившиеся данные отправляются на вход softmax или logistic regression функции, которая уже делает финальное предсказание \(\hat{y}\):