Функция ReLU задаётся формулой:
\[f(x)= \begin{cases} x, &x>0 \\ 0, &x\le 0 \end{cases} \]Частная производная этой функции равна единице в тех случаях, когда \(x > 0\). Это означает, что при использование такой активационной функции в глубокой сети, не происходит вымывания градиента.
В то же время, ReLU может быть источником проблем во время процесса оптимизации, поскольку градиент этой функции равен нулю даже в тех случаях, когда нейрон неактивен. Это может привести к тому, что нейрон никогда не буден активирован, а градиентный алгоритм не произведёт подстройки весов нейрона, который не был никогда активирован. То есть, если сеть столкнётся с константным нулевым градиентом, как и в случае вымывания градиента, обучение будет идти слишком медленно.
Для борьбы с этой проблемой можно использовать слегка модифицированную функцию, под названием LeakyReLU:
\[f(x)= \begin{cases} x, &x>0 \\ 0.01x, &x\le 0 \end{cases} \]У такой функции будет маленький ненулевой градиент в том случае, когда нейрон достиг насыщения и неактивен.
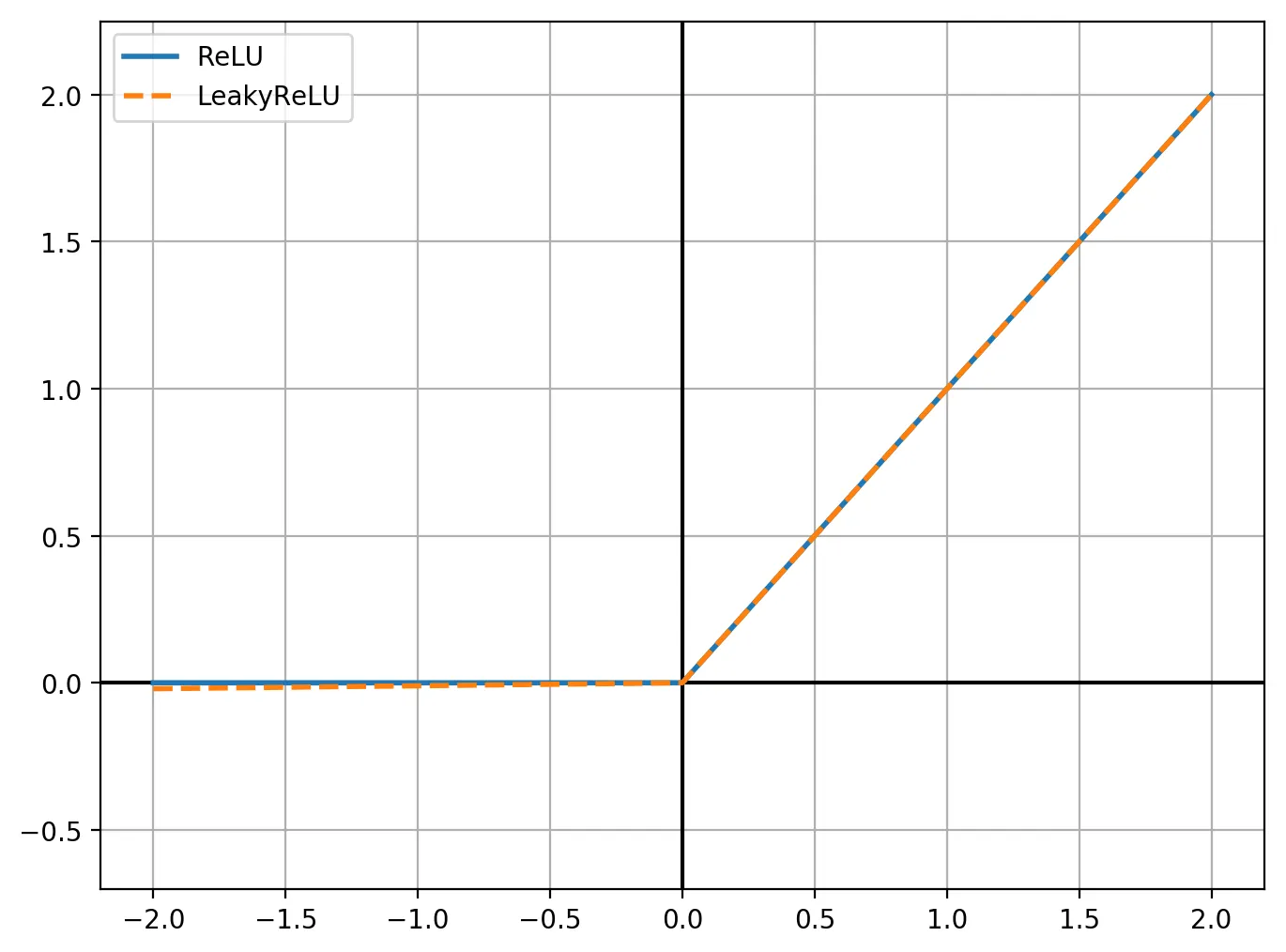
На графике эти функции выглядят похоже, за исключением того, что LeakyReLU при \(x\) меньше нуля, имеет небольшое ненулевое значение: