Норма Фробениуса матрицы вычисляется путем извлечения квадратного корня из суммы квадратов всех ее элементов:
\[\|A\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^2}\]Для простоты восприятия возьмем квадратную матрицу размером 2х2:
\[ \begin{bmatrix} 3 & 8 \\ 5 & 3 \end{bmatrix} \]Посчитаем норму Фробениуса этой матрицы, которая будет равна приблизительно 10.35:
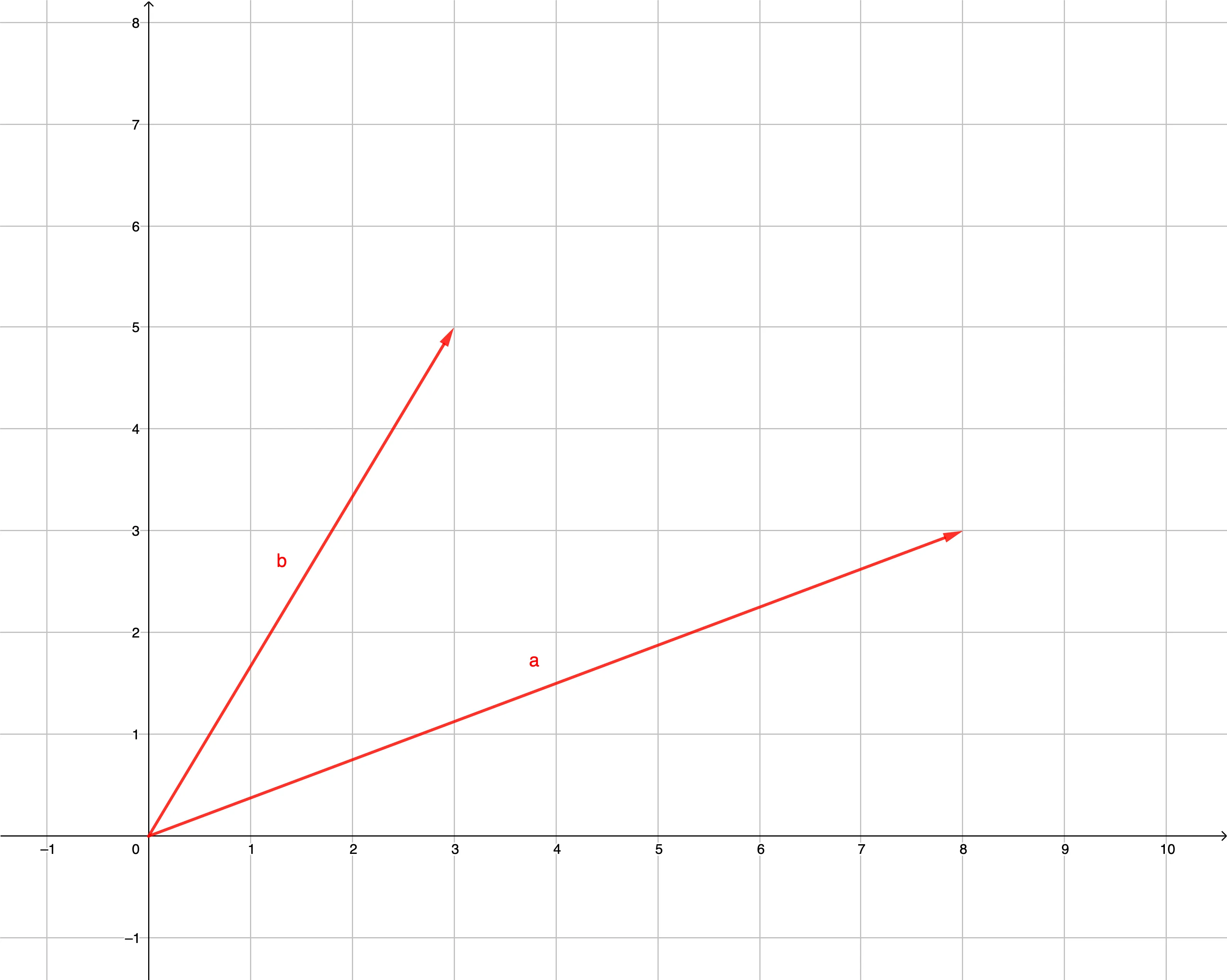
\[\|A\|_F = \sqrt{3^2 + 5^2 + 8^2 + 3^2}\approx 10.35\]Вот так выглядят векторы столбцов нашей матрицы на графике:
Далее нам понадобится длина обоих векторов, посчитать которую можно по теореме пифагора:
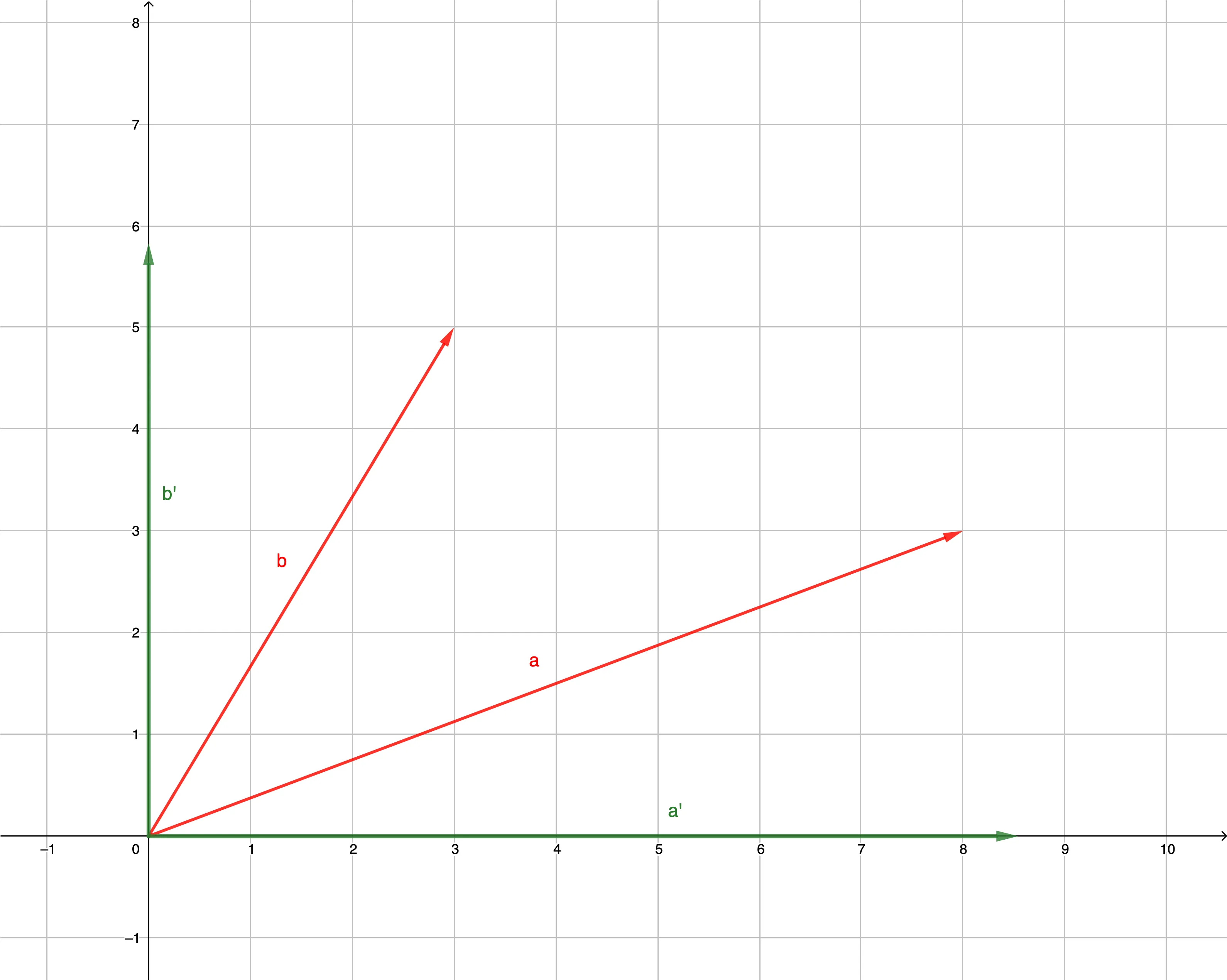
\[ \begin{aligned} |a| &= \sqrt{8^2 + 3^2} \approx 8.544 \\ |b| &= \sqrt{3^2 + 5^2} \approx 5.831 \end{aligned} \]Затем отобразим на графике два ортогональных вектора \(\mathbf{a}'\) и \(\mathbf{b}'\) той же длины, что исходные векторы \(\mathbf{a}\) и \(\mathbf{b}\):
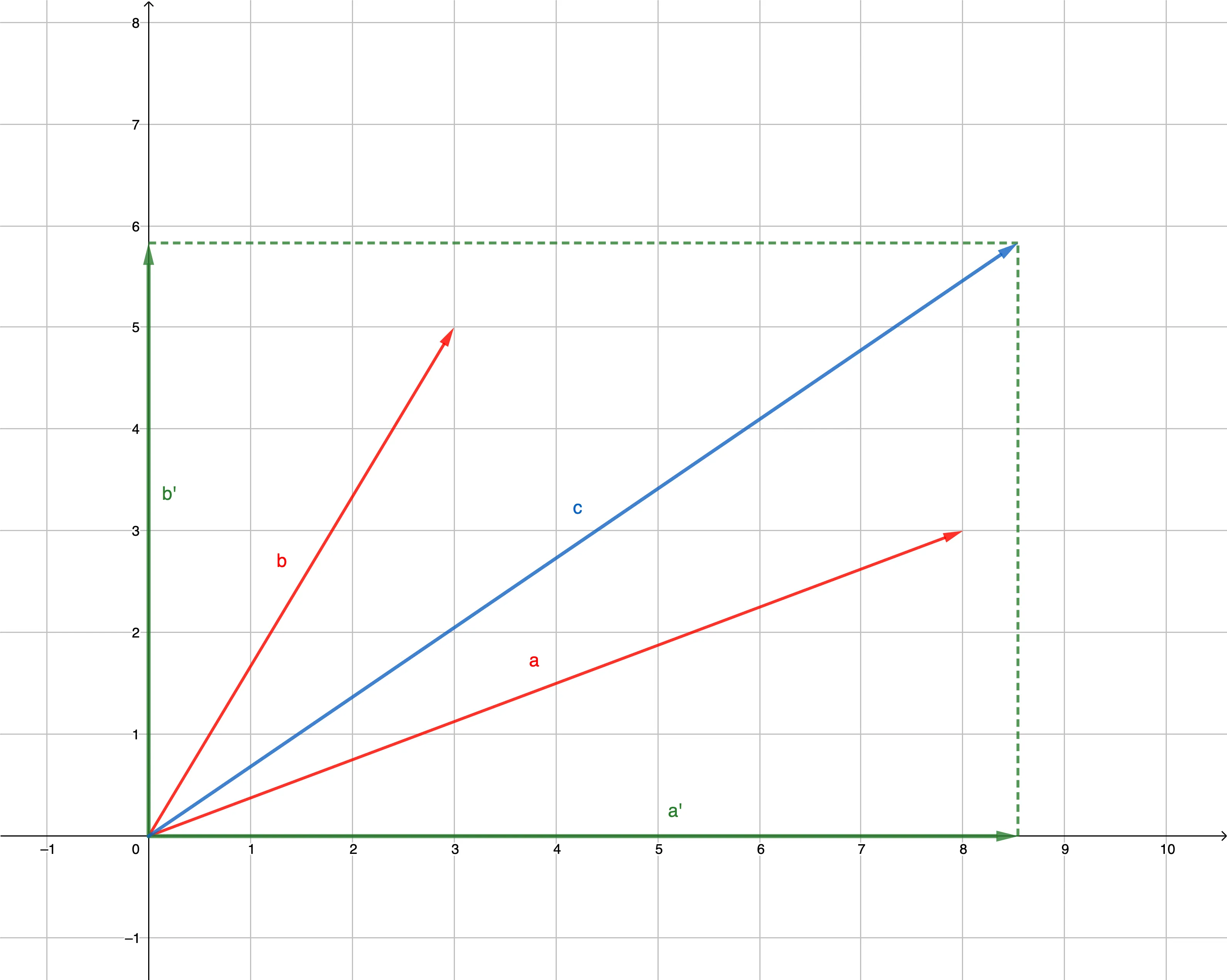
И затем сложим эти векторы по правилу параллелограмма:
Длина получившегося вектора \(\mathbf{с}\) как раз и будет равна норме Фробениуса нашей исходной матрицы.