Формально аффинное множество определяется так:
Множество \(X\subseteq \mathbb{R}^n\) называется аффинным, если вместе с любой парой точек \(x_1, x_2 \in X\) оно содержит все точки вида
\[x_\theta = \theta x_1 + (1-\theta)x_2\]где \(\theta \in \mathbb{R}\).
Другими словами, если мы возьмем любые две точки из такого множества, то окажется, что прямая, которая их соединяет, также принадлежит этому множеству.
Рассмотрим такой простой пример: пусть наше аффинное множество — это прямая, описываемая уравнением
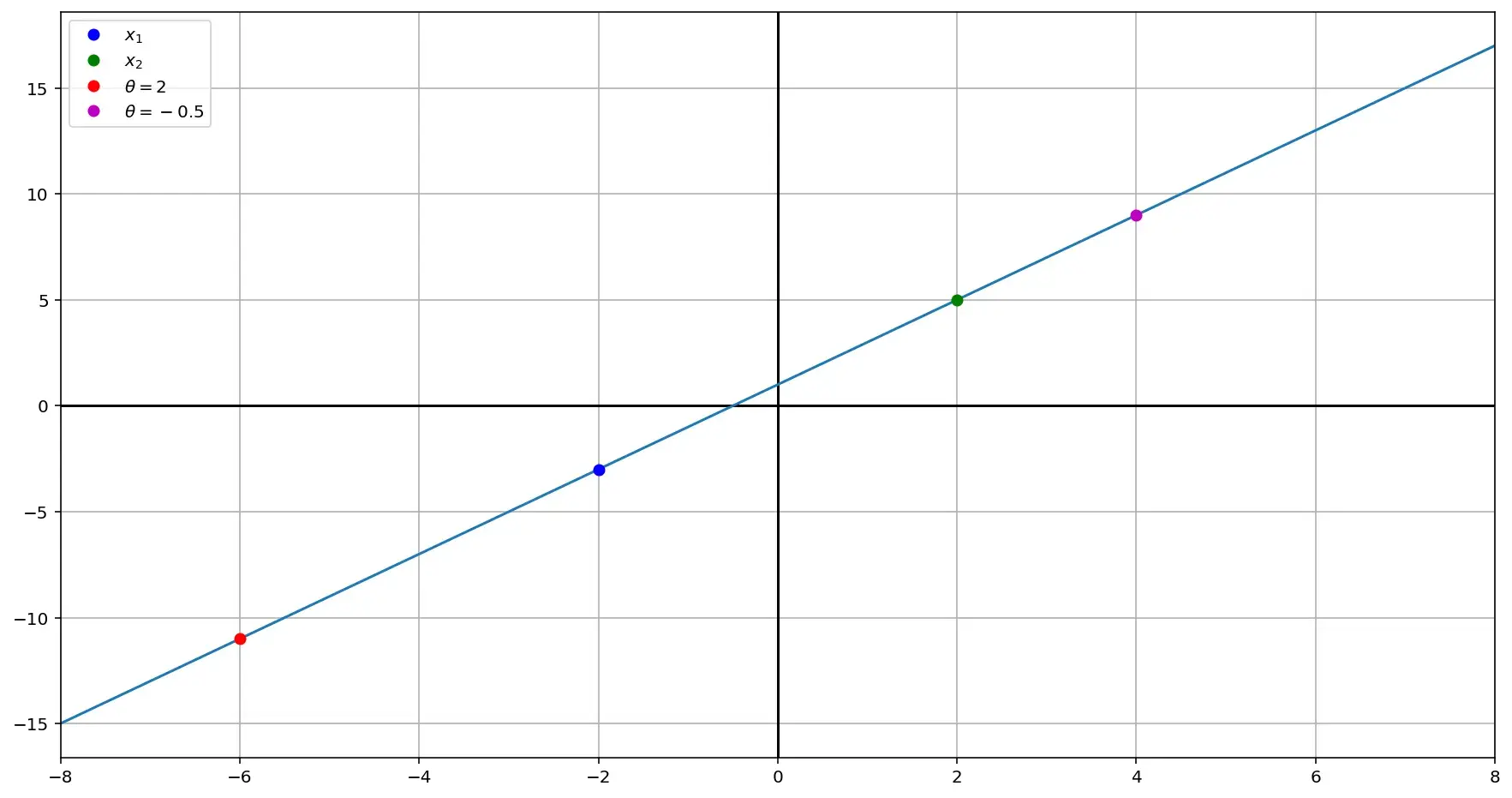
\[y = 2x +1\]Возьмем \(x_1=-2\), а \(x_2=2\).
Определение аффинного множества утверждает, что какой бы коэффициент \(\theta\) мы ни взяли, получившаяся точка окажется на той же прямой.
Для примера определим два разных коэффициента \(\theta\) и поглядим, как ведут себя точки. Пусть значения будут 2 и -0.5, тогда получившиеся точки \(x_θ\) будут иметь координаты (-6, -11) и (4, 9) и, если мы их построим на графике, то увидим, что они чудесным образом оказываются на той же самой прямой:
что и показывает верность определения.
Примерами аффинных множеств будут:
- \(\mathbb{R}^n\), прямая, гиперплоскость
- точка, \(\varnothing\) — пустое множество
- решение системы линейных уравнений
Справедливость последнего можно доказать по определению аффинного множества.
Возьмем две точки \(x_1, x_2 \in X\) и любой коэффициент \(\theta \in \mathbb{R}\). Проверим, чему будет равно \(Ax_θ\):
\[Ax_\theta = A\big(\theta x_1 + (1 - \theta)x_2\big) =\]раскроем скобки:
\[= \theta Ax_1 + (1- \theta)Ax_2 = \]Теперь смотрим внимательно на то что получилось: \(Ax_1\) лежит в нашем множестве \(X\), а значит можно сказать, что \(Ax_2\) — это \(b\). Аналогично и \(Ax_2\) лежит в множестве \(X\), а значит \(Ax_2\) — тоже \(b\). Подставим вместо них \(b\):
\[=\theta b + (1-\theta)b = b\]Это означает, что \(x_θ\) лежит в множестве \(X\), а это и говорит нам о том, что множество \(X\) — аффинное.